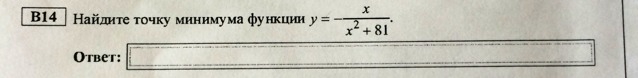Помогите тема 10 класса!математика

Минимум/максимум функции достигается в точках, где её производная обращается в ноль. Найдем эти точки.

Поскольку знаменатель дроби никогда не обращается в ноль, мы можем разделить на него обе части уравнения.

Функция y(x) имеет знак, зависящий от знака х. Мы ищем минимум, следовательно нам подходит область, где функция имеет отрицательные значения, т.е. x<0.
Возвращаясь к найденным значениям, выбираем x=-9 в качестве точки минимума функции. Значение функции в этой точке вычисляем как y(-9):

блин у меня 9 ответ