Решите задачу и приложите рисунок:

На сторонах AB, BC и AC треугольника ABC взяты соответственно точки M, D и К так, что АМ:МВ=2:3, AK:KC=2:1, BD:DC=1:2. В каком отношении МК делит отрезок AD?

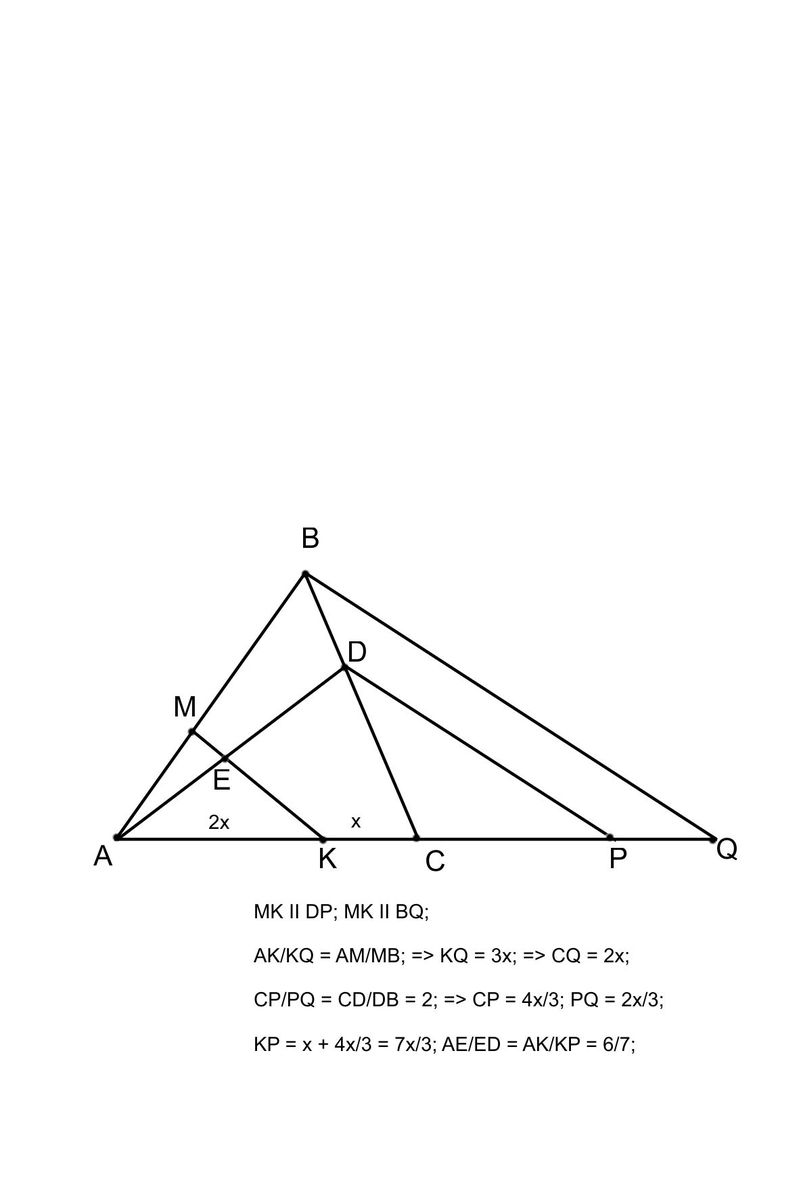
Пусть точка пересечения AD и MK обозначена E.
Если провести прямые DP II MK; BQ II MK; точки P и Q лежат на продолжении AC за точку C, и обозначить KC = x; то
AK = 2x;
Далее, из подобия треугольников AMK и ABQ
AK/KQ = AM/MB = 2/3;
KQ = 3x;
Поэтому CQ = 2x; 
Из подобия треугольников CDP CBQ
CP/PQ = CD/DB = 2; 
поэтому CP = (2/3)*CQ = 4x/3; KP = KC + CP = 7x/3;
из подобия треугольников AEK и ADP
AE/ED = AK/KP = 2x/(7x/3) = 6/7;
вроде так, проверяйте... такие задачи решаются тем же методом, каким доказывается прямая теорема Менелая.