Предмет: Геометрия
Автор: nastyabondaruk
Вопрос задан 9 лет назад

< >

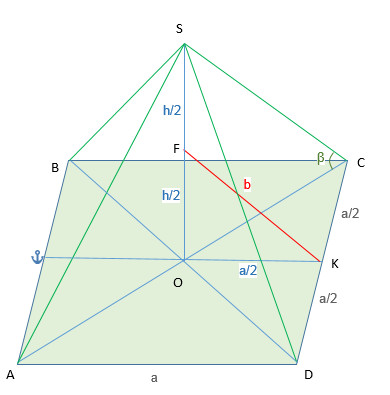
Боковое ребро правильной четырехугольной пирамиды образует с плоскостью основания угол β Отрезок соединяющий середину высоты пирамиды и середину бокового ребра равна в. найдите объем пирамиды

Ответы

Ответ дал: Аноним

0

По определению
tgβ=OS/OC=h/OC
OC=h/tgβ
В основании правильной четырехугольной пирамиды квадрат. Значит, треугольник OCK прямоугольный равнобедренный. По т.Пифагора
OC²=(a/2)²+(a/2)²=a²/4+a²/4=a²/2
OC=a/√2
$frac{a}{ sqrt{2} } = frac{h}{tg beta } \ a= frac{h sqrt{2} }{tg beta }$
Треугольник OFK прямоугольный. По т.Пифагора
$b^2=( frac{h}{2})^2+ ( frac{a}{2})^2 \ b^2=( frac{h}{2})^2+ ( frac{h sqrt{2} }{2tg beta })^2 \ b^2=frac{h^2}{4}+ frac{h ^2 }{2tg^2 beta } \ b^2=h^2(frac{tg^2 beta +2 }{4tg^2 beta }) \ b=h sqrt{frac{tg^2 beta +2 }{4tg^2 beta }} \ b=h frac{sqrt{tg^2 beta +2} }{2tg beta } \ h= frac{2b,tg beta }{sqrt{tg^2 beta +2}}$
Тогда
$a= frac{2 sqrt{2}* b,tg beta }{tg betasqrt{tg^2 beta +2}}= frac{2 sqrt{2}* b }{sqrt{tg^2 beta +2}}$
Формула объема правильной четырехугольной пирамиды
$V= frac{1}{3} ha^2= frac{1}{3} frac{2b,tg beta }{sqrt{tg^2 beta +2}}( frac{2 sqrt{2}* b }{sqrt{tg^2 beta +2}})^2=frac{16b^3,tg beta }{3(tg^2 beta +2)^{3/2}}$

Приложения:

Похожие вопросы

Русский язык

2 года назад

Помогите придумать ещё 3 предложения вот текст в реке амур шла кета.на берег спустилась медведица с медвежонком и стала ловить рыбу.она

Русский язык

2 года назад

Вставьте прощенные в словах буквы и подходящие по смыслу предложил для связи слов в словосочетаниях. Спросить у кого? Учителя, подъехал - ? деревне, пр-к- тился- ? трактире, пр-л-тал - ? столицей,

Математика

7 лет назад

Добуток чисел m і n дорівнює 70. Коли до множника m додали 2 й знову виконали множення , то добуток щбільшився на 28. Знайди число m і n.

Алгебра

7 лет назад

решите уравнение: √(2x-14)-cosx=x-√(7-x)

Математика

10 лет назад

Два велосипедиста одновременно выехали из пунктов А и В в одном направлении.Через сколько часов один велосипедист догонит другого,если скорости велосипедистов 18 км/ч и 12 км/ч,а расстояние между

Информатика

10 лет назад

В каком порядке будут расположены слова, если упорядочить их по УБЫВАНИЮ суммы кодов символов в таблице кодировки ASCII? 1) окно 2) кино 3) ника 4) конь 5) ночь

Математика

10 лет назад

Помогите мне пожалуйста разобраться с темой "Коэффициент" и "Подобные слагаемые"..Вообще не поняла эту тему. Объясните с примера.

Биология

10 лет назад

В чем сходства и различия белком и углеводов?