Вычислить площадь фигуры, ограниченную линиями: y² = 2x, y=3x.

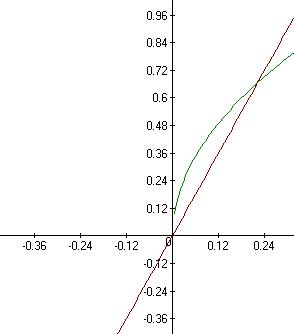
y=√2x   y=3x
√2x=3x   9x^2-2x=0   x1=0   x2=2/9

пределы интегрирования от 0 до 2/9

площадь по формуле Ньютона-Лейбница равна в пределах от 0 до 2/9

инт [(2x)^(1/2)] - инт [3x] =[2√2 *(√х)^3]/3 - (3x^2)/2

подставив пределы интегрирования, получим:

(2^3)/(27*3) - 2/27 = 2/81