Предмет: Математика
Автор: margaritaleus
Вопрос задан 9 лет назад

< >

найдите область определения функции y=√(12-x^2-x)/√(x+3)

Ответы

Ответ дал: Аноним

0

$y=frac{ sqrt{12-x^2-x} }{ sqrt{x+3} }$

1. Корень как всегда больше или равно нулю, но знаменатель не должен быть равен 0

$left { {{12-x^2-x geq 0} atop {x+3 geq 0}}atop {x+3 neq 0} right. \ left { {{x^2+x-12 leq 0} atop {x+3>0}} right.$

$x^2+x-12 leq 0 \$

1. Рассмотрим функцию и определим область определения функции:

$y=x^2+x-12 \ D(y)=R$

2. Определим нули функции

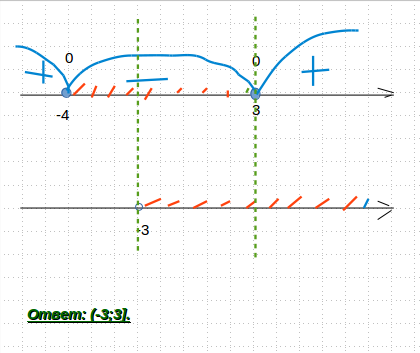
$x^2+x-12=0 \ D=b^2-4ac=1^2-4*1*(-12)=1+48=49 \ sqrt{D} =7 \ x_1= frac{-b+ sqrt{D} }{2a}= frac{-1+7}{2} =3 \ x_2= frac{-b- sqrt{D} }{2a}= frac{-1-7}{2} =-4$

3. Общие решения на промежутке смотреть во вложения.

$left { {{(x+4)(x-3) leq 0} atop {x >-3}} right.$

$OTBET:(-3;3]$

Приложения:

Ответ дал: margaritaleus

0

спасибо большое)

Ответ дал: Аноним

0

Обращайтесь)

Похожие вопросы

Русский язык

2 года назад

выпиши форму слов роза и куст и обозначь окончания

Русский язык

2 года назад

Исправьте предложения. Объясните с чем связана допущенная лексическая ошибка, определите ее вид. 1) Первая премьера этого спектакля состоялась в декабре. 2)В парке запрещен выпас собак. 3)День

Математика

7 лет назад

Если диаметр окружности равен 15 см , то радиус этой окружности равен ?

Геометрия

7 лет назад

Помогите пожалуйста решить

Литература

10 лет назад

Составить описать одного из водоёмов своего края(название,растения и животные водоёма,использование водоёма человеком).Составь две-три цеи питания,которые сложились в этом водоёме.

Математика

10 лет назад

Объем аквариума равен 120 000см в кубе,найдите высоту аквариума,если длина 60 см.а ширина 40

География

10 лет назад

Найдите ошибку: вечная мерзлота занимает до 50% территории России; летом в мерзлотных районах оттаивает только верхний, до 1 м, слой земной коры; мерзлотные районы очень удобны для строительства

Биология

10 лет назад

от чего зависит цвет кожи человека?