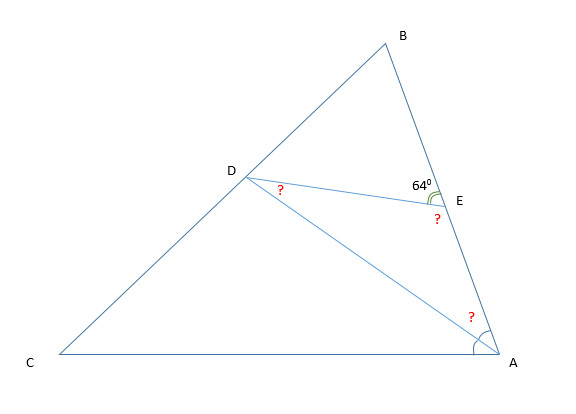
Отрезок AD- биссектриса треугольника ABC. Из точки D проведена прямая , пересекающая сторону AB в точке E так , что AE=ED. Найдите углы треугольника AED если уголBED=64*. ( если можно с рисунком)

Для обозначения знака угла будем использовать знак <

<DEA и <BED смежные. Поэтому
<DEA=180° - <BED=180°-64°=116°
Поскольку AE=ED, то треугольник AED равнобедренный, поэтому
<EDA=<DAE
Сумма всех углов треугольника равна 180°, поэтому
<EDA=<DAE=(180°-<DEA):2=(180°-116°):2=32°
Ответ: 32°; 32°; 116°