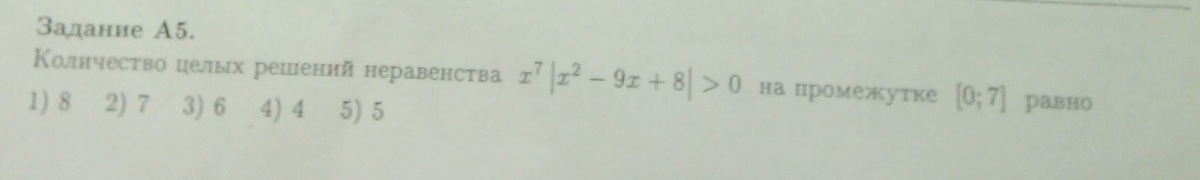помогите пожалуйста решить срочно

Раскроем правильно модуль, получим две системы:
1) 




x∈(-бесконечность;1)U(8; +бесконечность)
Чтобы второе неравенство было верным, необходимо, чтобы x^7 было больше нуля (т.е. x>0). Объединим оба решения, получим: x∈(0;1)U(8; +бесконечность)
Наложим условие, что корни необходимо искать на отрезке, получим:
x∈(0;1) - точка 0 не входит в решение, т.к. неравенство строгое.
На этом интервале целых решений нет.

2) 

Решением первого неравенства является: x∈(1;8)
Чтобы второе неравенство было верным, необходимо, чтобы x^7 было больше 0 (т.е. x>0). Объединяем оба решения, получаем: x∈(1;8).
Наложим условие, что корни необходимо искать на отрезке, получим: x∈(1;7]
Перечислим целые решения: x=2, 3, 4, 5, 6, 7 (всего 6 целых решений)

Ответ: 6 целых решений