Предмет: Математика
Автор: danieladi
Вопрос задан 9 лет назад

помогите пожалуйста решить два уравнения . в ответ надо записать наибольший отрицательный корень уравнения,выраженный в градусах
я знаю что сначала надо уравнение поделить на косинус квадрат икс.но у меня там дальше не стыкуется

Приложения:

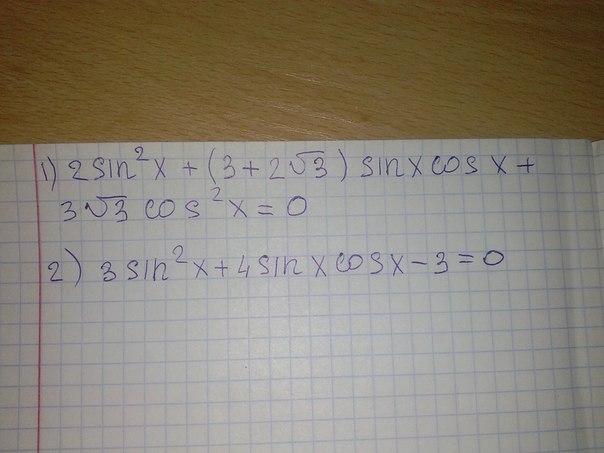
Ответы

Ответ дал: Аноним

$2sin^2x+(3+2 sqrt{3})sinx,cosx+3 sqrt{3}cos^2x=0;$
Для того, чтобы перейти к единой тригонометрической функции, нужно обе части уравнения разделить или на sin²x (получая tg²(x) и tg(x)), или на cos²(x) (получая ctg²(x) и ctg(x)). Допустим, делим на cos(x); при этом возникает ОДЗ: cos(x)≠0.
$2tg^2x+(3+2 sqrt{3})tgx+3 sqrt{3}=0;$
Делаем замену переменной: y=tg(x) (1)
$2y^2+(3+2 sqrt{3})y+3 sqrt{3}=0; \ D=(3+2 sqrt{3})^2-4*2*3 sqrt{3}=9+12 sqrt{3}+12-24 sqrt{3}=21-12 sqrt{3}= \ 9-2*2*3 sqrt{3}+12=3^2-2*3*2 sqrt{3}+(2 sqrt{3})^2=(3-2 sqrt{3})^2; \ sqrt{D}=3-2 sqrt{3} \ y_1= frac{-(3+2 sqrt{3})-(3-2 sqrt{3})}{2*2}= frac{-6}{4}=- frac{3}{2}; \ y_2=frac{-(3+2 sqrt{3})+(3-2 sqrt{3})}{2*2}= frac{-4 sqrt{3}}{4}=- sqrt{3};$
Подставляем найденные решения в (1) и находим x=arctg(y)
$x_1=arctg(y_1)=arctg(- frac{3}{2})=-arctg(1.5); \ x_2=arctg(y_2)=arctg(- sqrt{3})=-arctg(sqrt{3}); \ 1.5^2=2.25 to -arctg( sqrt{2.25})>-arctg( sqrt{3})$
Требуется записать наибольший отрицательный корень уравнения, выраженный в градусах. Наибольшим из отрицательных чисел является то, которое по абсолютной величине меньше, т.е. arctg(1.5), но оно не выражается точно в градусной мере. Если сделать предположение, что имелся в виду наибольший по абсолютной величине отрицательный корень, то ввиду наличия периода функции, равного π, он уходит в минус бесконечность. -arctg(1.5) ≈ -56.31 град, -arctg(√3) = -60 град.
По моему мнению, если буквально понимать условие, ответ -56.31 градуса.

$3sin^2x+4sinx,cosx-3=0; \ 3(1-cos^2x)+4sinx,cosx-3=0; 3-3cos^2x+4sinx,cosx-3=0; \ 3cos^2x-4sinx,cosx=0; cosx(3cosx-4sinx)=0; \ cosx_1=0 to x_1=arccos(0)pm pi k=90^circpm180^circ*k; \ 3cosx_2-4sinx_2=0; 4sinx_2=3cosx_2; 4frac{sinx_2}{cosx_2}=3; tgx_2= frac{3}{4}; \ x_2=arctg frac{3}{4}pm pi k approx 36.87^circpm180^circ *k$
Здесь наибольший отрицательный корень -90 градусов.

Похожие вопросы

Русский язык

2 года назад

Вставить пропущенные буквы знаки препинания. Ч__рной зав__сти п__лна,Бросив зерк__льце (под) ла__ку,Позв__ла (к) себе Чернавку.И наказывает ей,Сенной девушке своей,Весть ц__ревну (в) глу[ш]

Другие предметы

2 года назад

похожи но разные лягушка ижаба чем отлечаются

Геометрия

7 лет назад

На площині дано трапецію і точку поза нею, яка віддалена від кожної із сторін на відстані 13см, знайти відстань від цієї точки до площини трапеції. Якщо більше сторона трапеціх дорівнює 6 см і 8 см а

География

7 лет назад