Предмет: Физика
Автор: lelkasorokina
Вопрос задан 9 лет назад

Радиус-вектор частицы изменяется по закону: r = 5t2i + j + 2tk. Определить: а) уравнение траектории частицы, б)
скорость и ускорение частицы в момент времени t0= 1 с, в)
касательное и нормальное ускорение точки в этот же момент времени, а также
радиус кривизны траектории R.

Ответы

Ответ дал: Аноним

a)
Из закона видно, что
x=5t²
y=1 (от t не зависит)
z=2t
Тогда
t=z/2
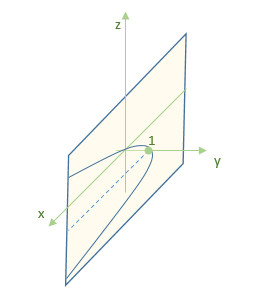
x=5(z/2)²=1.25z² - парабола
б)
Формула скорости
$v= frac{dr}{dt} \ v=10ti+2k \ v(1)=10i+2k \ |v(1)|= sqrt{10^2+2^2} = sqrt{104}=2 sqrt{26}$
Ускорение
$a= sqrt{a_{ tau}^2+a_n^2} \ a_{ tau}= frac{dv}{dt} =10i \ |a_{ tau}|=10 \ a_{ tau}(1)=10$
Формула радиуса кривизны
$R= frac{vt}{2 pi } \ R= frac{2 sqrt{26} }{2 pi } =frac{ sqrt{26} }{ pi }$
Тогда центростремительное ускорение
$a_n= frac{v^2}{R} \ a_n= frac{(2 sqrt{26} )^2}{ frac{ sqrt{26} }{ pi } }=4 pi sqrt{26}$
Полное ускорение
$a= sqrt{10^2+(4 pi sqrt{26})^2 } = sqrt{100+416 pi ^2}$
Ответ: 2√26 м/с; √(100+416π²) м/с²
в)
Искомые значения были определены в предыдущем пункте
Ответ:
$a_{ tau}=10 \ a_n=4 pi sqrt{26} \ R= frac{ sqrt{26} }{ pi }$

Приложения: