Две противоположные стороны
выпуклого четырехугольника лежат на перпендикулярных прямых. Докажите, что
расстояние между серединами двух других сторон четырехугольника равно
расстоянию между серединами его диагоналей.

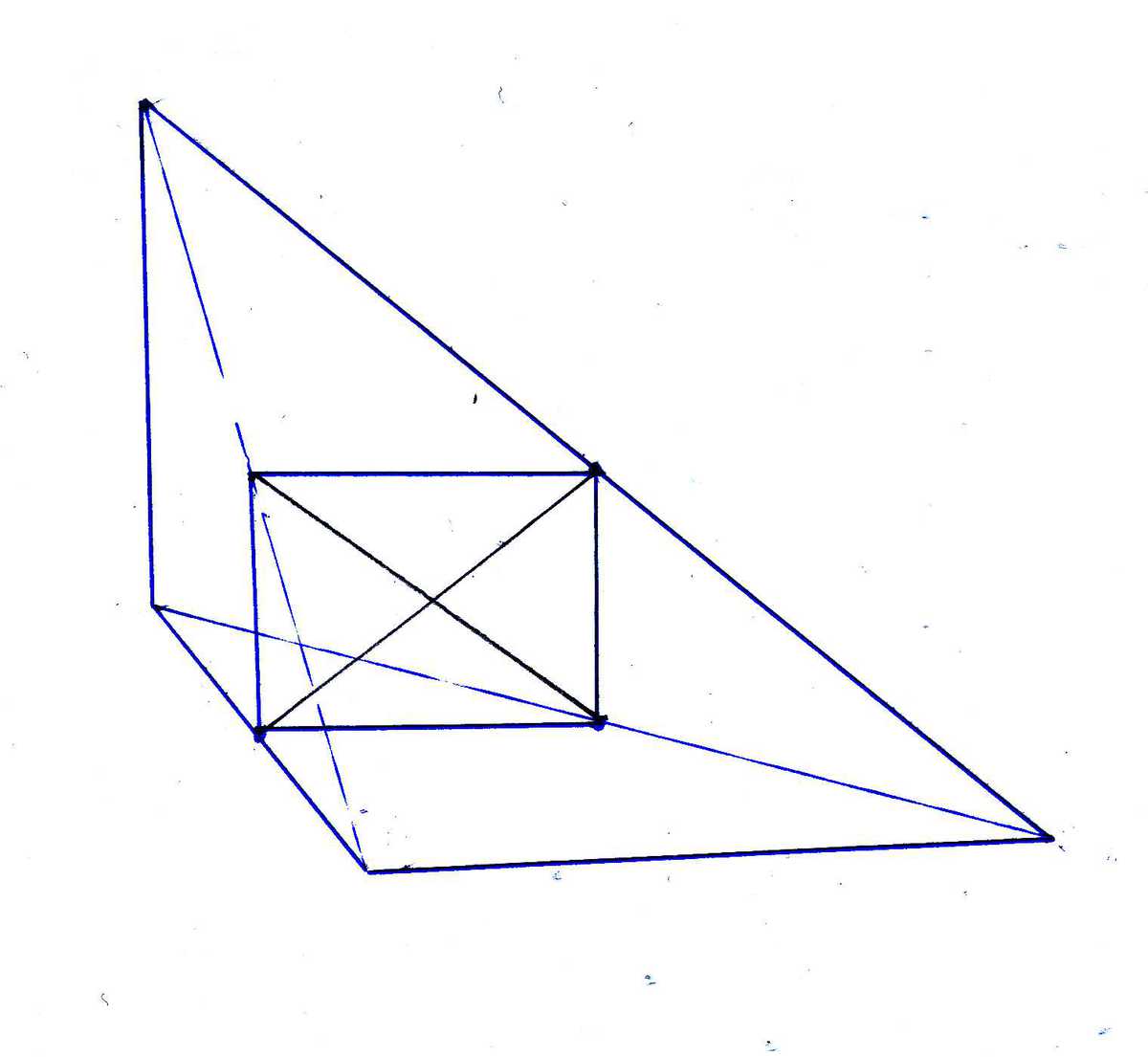
Если последовательно соединить середины сторон и середины диагоналей, получится прямоугольник - каждая сторона его параллельна одной из взаимно перпендикулярных сторон четырехугольника. И равна её половине :) - как средняя линяя.
Отрезки, про которые спрашивается в задаче - диагонали этого прямоугольника, поэтому они равны.

Вы как всегда блистательны.