В правильной
четырёхугольной пирамиде SABCD  M— середина ребра BC,
S — вершина. DM=6*√5, SM=√(292). Найдите высоту
пирамиды.

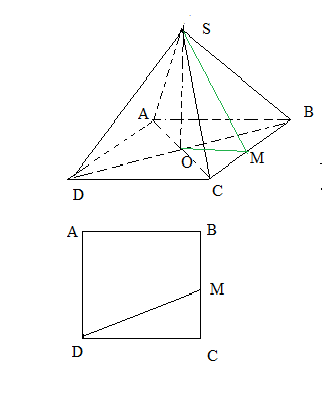
Рассмотрим основание пирамиды ( см. нижний рисунок)
Пусть сторона квадрата равна 2а, тогда МС=а,
По теореме Пифагора из треугольника МСD: MD²=MC²+CD²=a²+(2a)²=5a²
MD=a√5, а по условию 6√5, значит а=6
Сторона квадрата равна 12
Рассмотрим прямоугольный треугольник SOM:
по условию SM=√292, ОМ=1/2 АВ=6 см
По теореме Пифагора высота пирамиды SO²=SM²-OM²=(²√292)-6²=256
SO=14 cм