в треугольнике АВС Биссектриса AF и медиана ВМ перпендикулярны. Найти площадь треугольника АВС, если длина медианы равна m, а длина биссектрисы l.

Помогите,  пожалуйста.

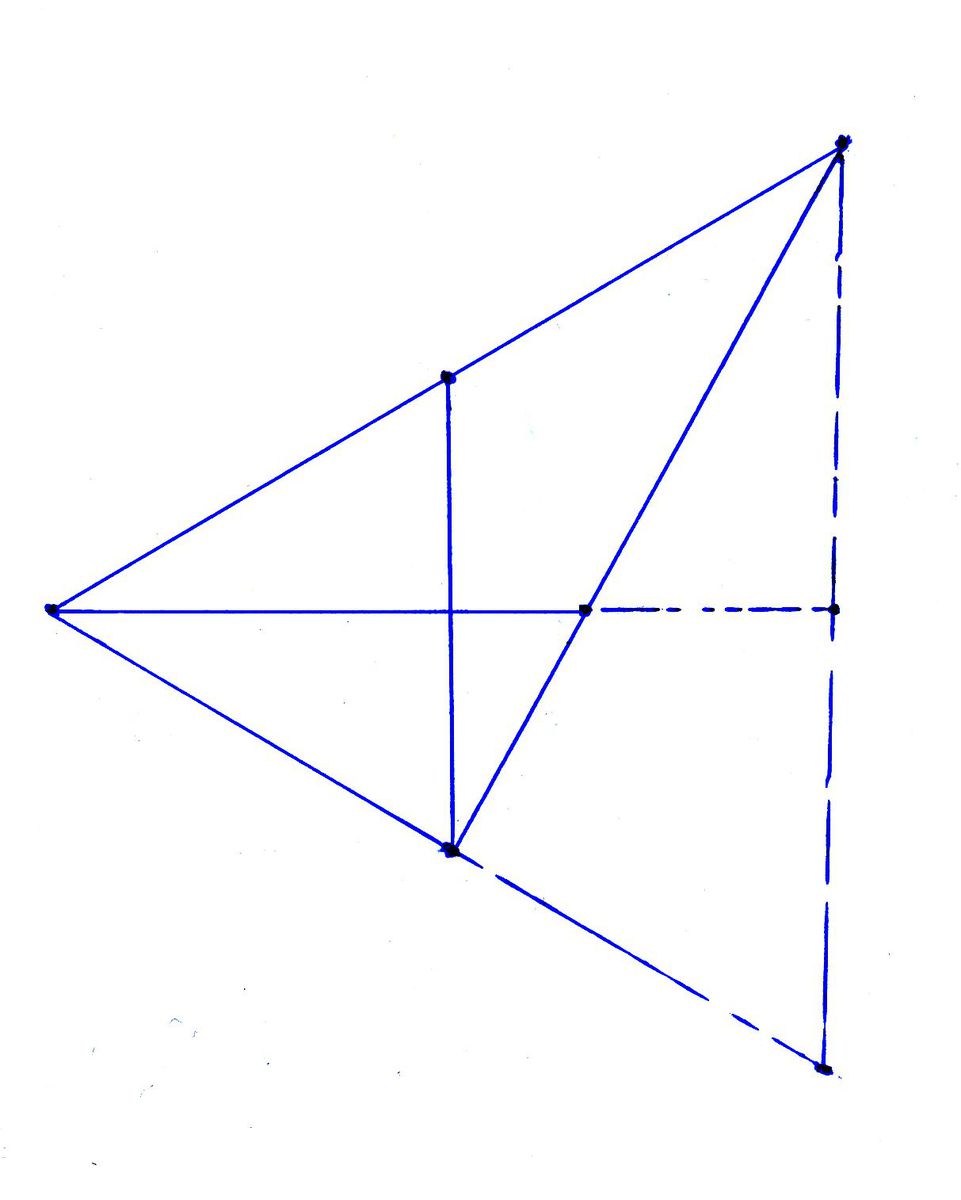
Я там добавил чертежик, на котором НАМЕРЕННО не поставил никаких обозначений - они только мешают. Эта задача как раз лучше всего решается именно так - надо внимательно посмотреть на чертеж :).
Исходный треугольник представлен сплошными линиями вместе с биссектрисой и медианой. Этот треугольник достраивается до равнобедренного (пунктирные линии), и биссектриса тоже продолжается до пересечения со стороной, которая параллельна медиане (исходного тр-ка).
В получившемся РАВНОБЕДРЕННОМ (биссектриса = высота) треугольнике медиана исходного треугольника играет роль средней линии, а биссектриса и сторона, к которой она проведена - медианы.
Если H - высота достроенного треугольника (частью которой является биссектриса исходного), то l = H*2/3; 
Площадь исходного треугольника очевидно равна половине площади достроенного, то есть ("основание" достроенного треугольника равно 2*m) 
S = m*H/2 = m*l*(3/2)/2 = (3/4)*m*l;

еще это тот случай, когда теорема Чевы оказывается не у дел :) Используя её, можно все найти, конечно, но это как травить фантой тараканов. Конечно, рано или поздно тараканы умрут от возмущения, но всё-таки это не самый простой способ :)