Окружность вписана в равнобедренную трапецию с острым углом 30 градусов. найдите отношение длины окружности к периметру трапеции
Ответы
Ответ дал:
0
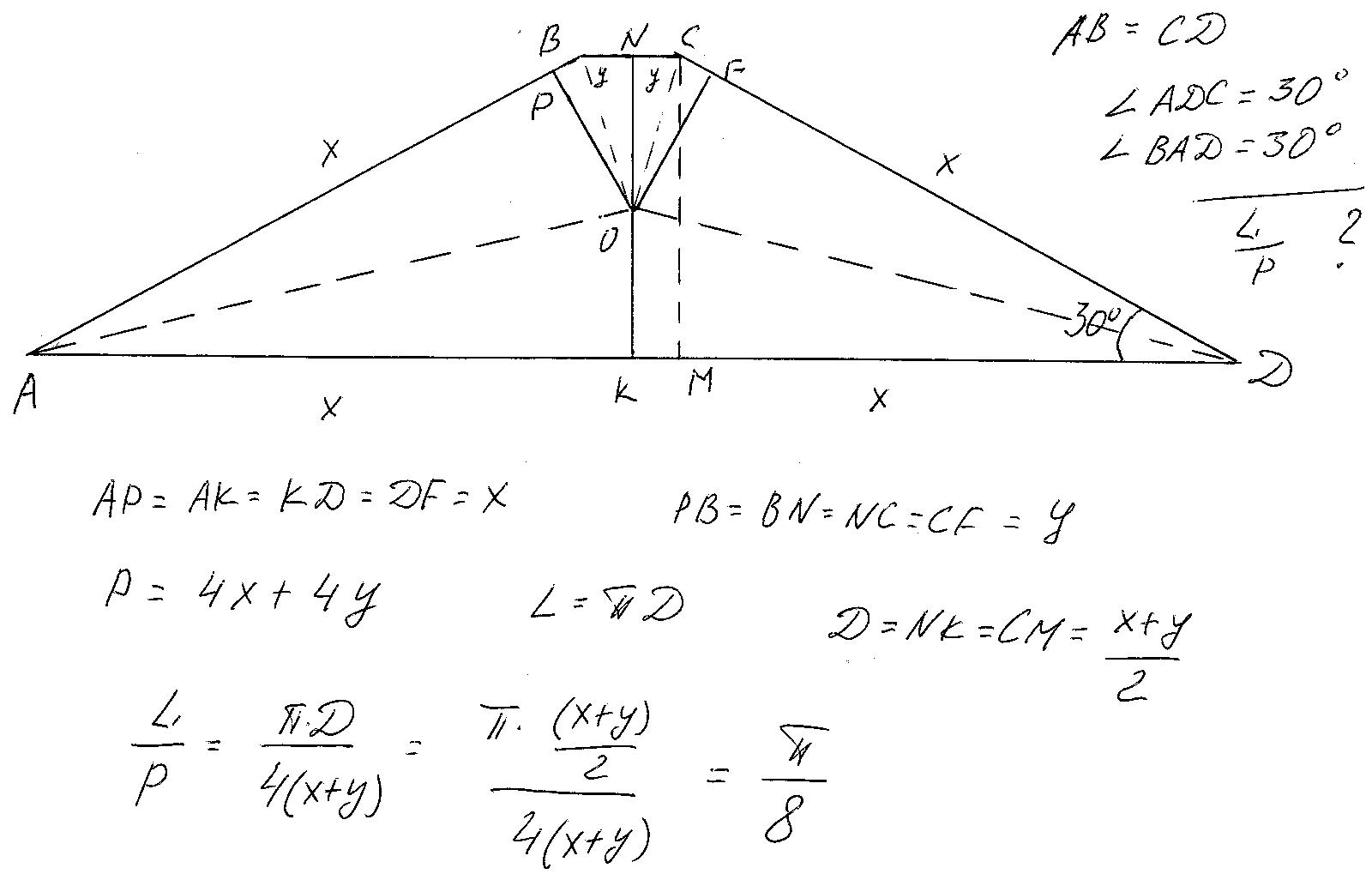
Обозначим трапецию АВСД(смотри рисунок).Проведём радиусы ОР, ОF, ОК. Диаметр вписанной окружности равен высоте трапеции NК=СМ=1/2 СД. Поскольку в прямоугольном треугольнике СМД сторона СМ лежит против угла 30 градусов.Далее рассмотрим треугольники АВО и АОК они равны как прямоугольные у которых гипотенуза АО -общая и катеты равны как радиусы. Аналогично доказываем и для остальных треугольников. Обозначаем равные стороны Х и У. И находим отношение L/Р="пи"/8.
Приложения:
Похожие вопросы
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад