Докажите, что функция f(x) чётная, если...
Только б)
Помогите разобраться, пожалуйста.
Приложения:
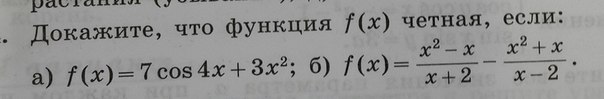
Ответы
Ответ дал:
0
Давай на первом примере. Функция чётная, если y(-x) = y(x)

Нужно учесть, что
cos(-x)=cos(x)
(-х)^2=x^2
Нужно учесть, что
cos(-x)=cos(x)
(-х)^2=x^2
Ответ дал:
0
f(x)=(x²-x)/(x+2) - (x²+x)/(x-2)
f(-x)=((-x)²-(-x))/(-x+2) - ((-x)²+(-x))/(-x-2)=
=(x²+x)/(-x+2) - (x²-x)/(-x-2)=
= -(x²+x)/(x-2) + (x²-x)/(x+2)=(x²-x)/(x+2) - (x²+x)/(x-2)=f(x)
Итак, f(-x)=f(x)
Следовательно, функция чётная
f(-x)=((-x)²-(-x))/(-x+2) - ((-x)²+(-x))/(-x-2)=
=(x²+x)/(-x+2) - (x²-x)/(-x-2)=
= -(x²+x)/(x-2) + (x²-x)/(x+2)=(x²-x)/(x+2) - (x²+x)/(x-2)=f(x)
Итак, f(-x)=f(x)
Следовательно, функция чётная
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад