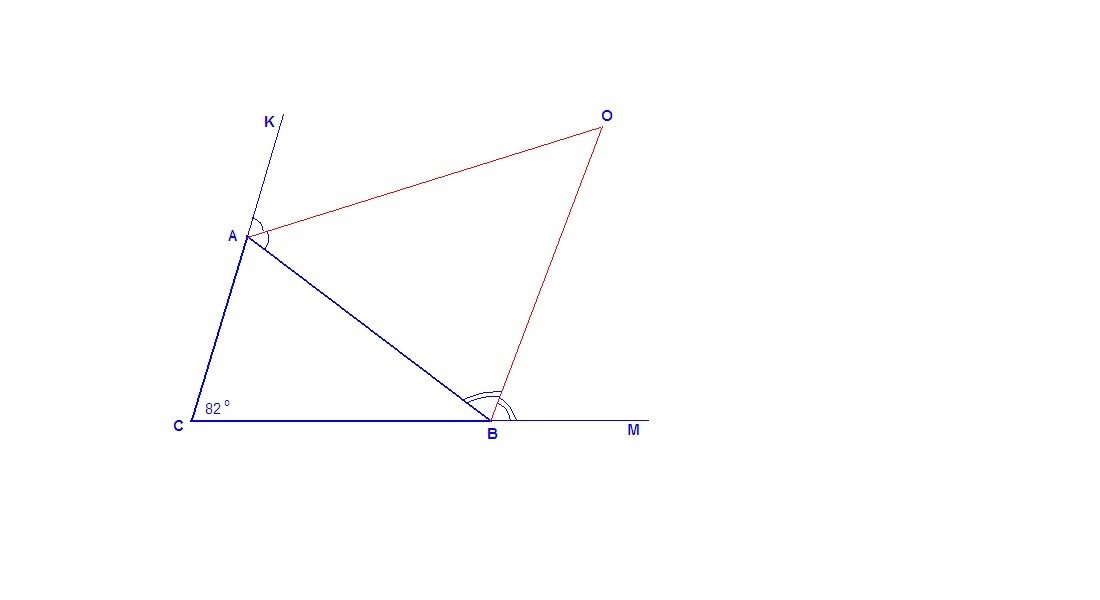
в треугольнике авс угол с равен 82 градуса . биссектрисы внешних углов при вершинах а и в пересекаются в точке о. найдите градусную меру угла аов

Из ΔАВС:
∠САВ + ∠СВА = 180° - 82° = 98°
Внешний угол смежный с внутренним, поэтому
∠КАВ = 180° - ∠САВ
∠МВА = 180° - ∠СВА
Сумма внешних углов при вершинах А и В:
∠КАВ + ∠МВА = 360° - (∠САВ + ∠СВА) = 360° - 98° = 262°
Так как АО и ВО биссектрисы,
∠ОАВ + ∠ОВА = 1/2(∠КАВ + ∠МВА) = 1/2 · 262° = 131°
Из ΔОАВ:
∠АОВ = 180° - (∠ОАВ + ∠ОВА) = 180° - 131° = 49°