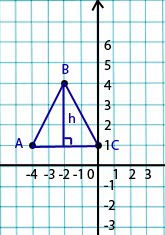
Докажите что треугольник АВС равнобедренный и найдите его площадь если вершины треугольника имеют координаты А(-4,1) В(-2,4) С(0,1)

Треугольник АВС
AB= {−2−(−4),4−1} = {2,3} 
AB=√(2²+3²)=√13

BC = {0−(−2),1−4} = {2,−3} 
BC=√(2²+(-3)²)=√13

CA = {−4−0,1−1} = {−4,0}
CA=√((-4)²+(0)²)=4

AB=BC - треугольник равнобедренный

h - высота проведенная из вершины B к основанию AC

Найдем по т.Пифагора высоту h

h²+4=13
h²=9
h=3
s=ah/2
s=3*4/2=6
Ответ: 6