Основанием пирамиды является равносторонний треугольник. Высота пирамиды 4(корень) 3

Каждое боковое ребро образует с плоскостью основания угол 45 гр

Найти сторону основания пирамиды.

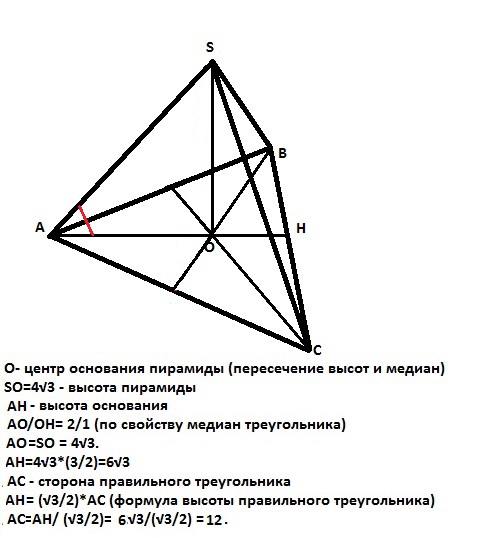
Данная нам пирамида правильная, так как каждое боковое ребро образует с плоскостью основания одинаковый угол.  Основание высоты правильной треугольной пирамиды находится в центре правильного треугольника (основания пирамиды). Центр равностороннего треугольника является точкой пересечения высот и медиан и делит медиану (высоту) в отношении 2:1, считая от вершины (свойство медианы).
Боковое ребро образует с плоскостью основания угол 45°, значит высота
пирамиды равна отрезку высоты основания пирамиды, считая от вершины, то есть она равна 2/3 высоты основания. Тогда высота основания равна 4√3*3/2=6√3.
Высота равностороннего треугольника (основания пирамиды) равна
h=(√3/2 )*a, где а - сторона треугольника (основания), отсюда а=6√3*2/√3=12.
Ответ: сторона основания пирамиды а=12.

откуда вышло 3/2 что-то я не поняла

Какие 3/2 ? В решении этого нет.