Найдите площадь равнобедренного треугольника по боковой стороне и высоте, опущенной на основание, которые равны соответственно 5 см и 2 см.
Ответы
Ответ дал:
0
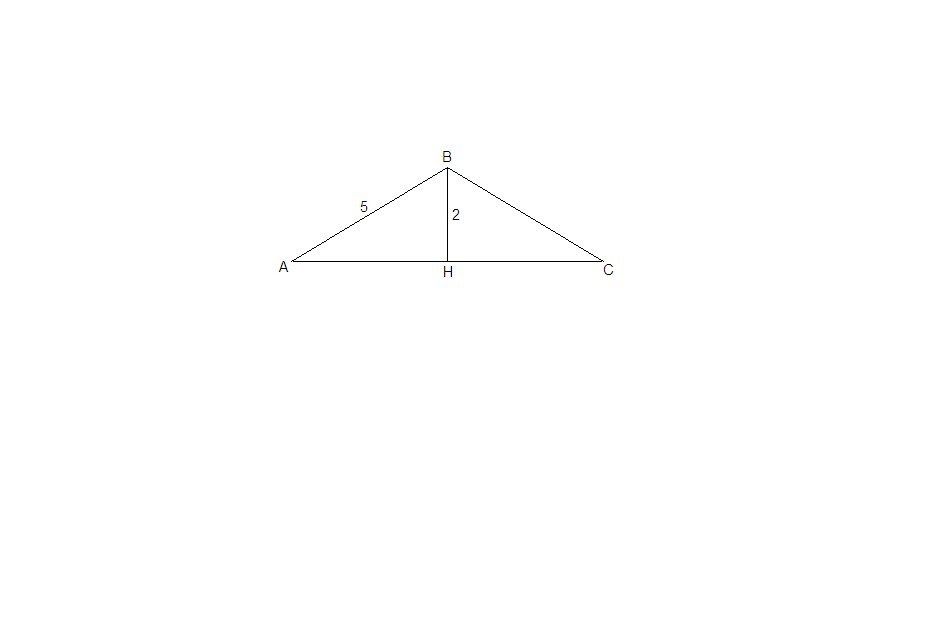
В треугольнике АВС:
АВ = ВС = 5 см,
ВН = 2 см - высота.
ΔАВН: ∠АНВ = 90°, по теореме Пифагора
АН = √(АВ² - ВН²) = √(25 - 4) = √21 см
В равнобедренном треугольнике высота, проведенная к основанию, является медианой, значит
АС = АН · 2 = 2√21 см
Sabc = AC · BH /2
Sabc = 2√21 · 2 / 2 = 2√21 см²
АВ = ВС = 5 см,
ВН = 2 см - высота.
ΔАВН: ∠АНВ = 90°, по теореме Пифагора
АН = √(АВ² - ВН²) = √(25 - 4) = √21 см
В равнобедренном треугольнике высота, проведенная к основанию, является медианой, значит
АС = АН · 2 = 2√21 см
Sabc = AC · BH /2
Sabc = 2√21 · 2 / 2 = 2√21 см²
Приложения:
Похожие вопросы
2 года назад
8 лет назад
8 лет назад
10 лет назад