Две соседние вершины и точка пересечения диагоналей квадрата лежат в пл-ти α. Доказать, что две другие вершины квадрата лежат в этой плоскости.
Ответы
Ответ дал:
0
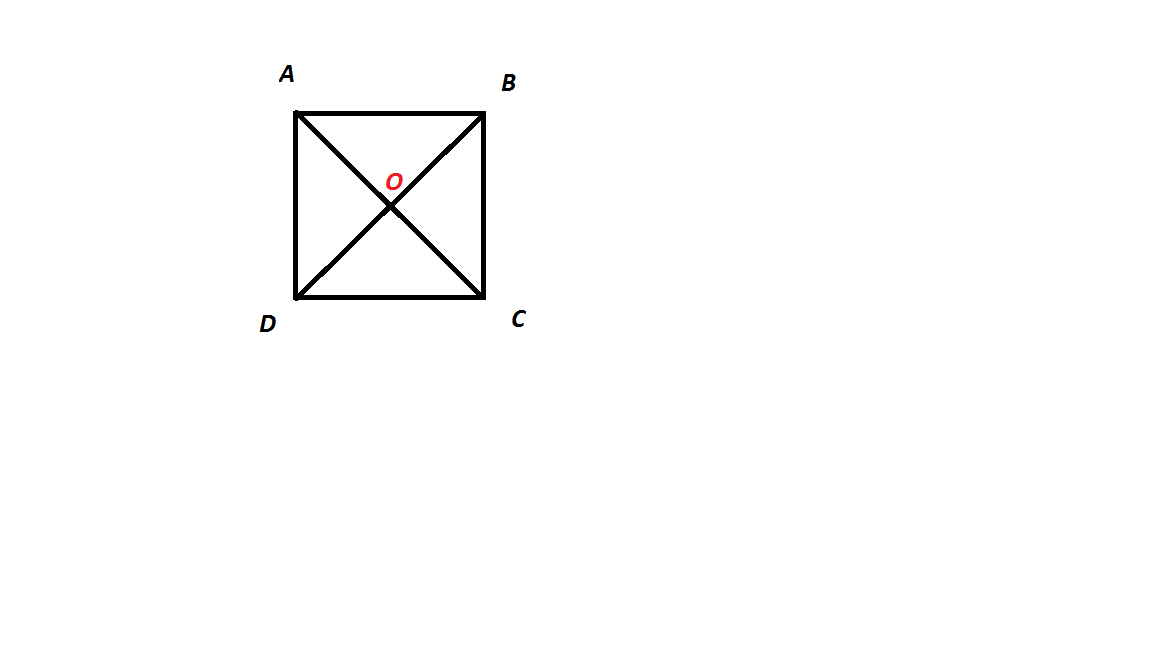
Точка D и C а так же О, лежат в плоскости.
РАссмотрим диагонал DB. B пренадлежит DO, а DO лежит в плоскости(так как две точки лежат в плоскости) => B лежит в плоскости.
Рассмотрим диагонал CA. A пренадлежит СO, а СО лежит в плоскости(так как две точки С и О лежат в плоскости) следовательно А лежит также в плоскости.
следовательно все вершины квадрата находятся в одной плоскости
это на основе теоремы: ЕСЛИ ДВЕ ТОЧКИ ПРЯМОЙ ЛЕЖАТ В ПЛОСКОСТИ,ТО ВСЕ ТОЧКИ ПРЯМОЙ ЛЕЖАТ В ЭТОЙ ПЛОСКОСТИ. вроде так звучит, удачи вам.
Приложения:
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад