Дана функция 
, где 
1. Найдите наибольшее и наименьшее значения функции на отрезке [0;2]
2. На каком отрезке функция принимает наибольшее значение, равное 25, наименьшее значение, равное 1?
3. Решите уравнение 
Ответы
Ответ дал:
0
1.
![D_{f(x)}=R, \
f'(x)= 3^{x}ln3, \
f'(x)=0, 3^{x}ln3=0, \
3^{x}=0, \
xinvarnothing; \
f(0)=3^{0}-2=-1; \
f(2)=3^{2}-2=7; \
minlimits_{xin[0;2]}f(x)=-1, maxlimits_{xin[0;2]}f(x)=7.](https://tex.z-dn.net/?f=D_%7Bf%28x%29%7D%3DR%2C+%5C%0Af%27%28x%29%3D+3%5E%7Bx%7Dln3%2C+%5C%0Af%27%28x%29%3D0%2C+3%5E%7Bx%7Dln3%3D0%2C+%5C%0A3%5E%7Bx%7D%3D0%2C+%5C%0Axinvarnothing%3B+%5C%0Af%280%29%3D3%5E%7B0%7D-2%3D-1%3B+%5C%0Af%282%29%3D3%5E%7B2%7D-2%3D7%3B+%5C%0Aminlimits_%7Bxin%5B0%3B2%5D%7Df%28x%29%3D-1%2C+maxlimits_%7Bxin%5B0%3B2%5D%7Df%28x%29%3D7.+ "D_{f(x)}=R, \
f'(x)= 3^{x}ln3, \
f'(x)=0, 3^{x}ln3=0, \
3^{x}=0, \
xinvarnothing; \
f(0)=3^{0}-2=-1; \
f(2)=3^{2}-2=7; \
minlimits_{xin[0;2]}f(x)=-1, maxlimits_{xin[0;2]}f(x)=7.")
2.
![f(x)=25, 3^{x}-2=25, \
3^{x}=27, \ 3^{x}=3^3, \ x=3; \
f(x)=1, 3^{x}-2=1, \
3^{x}=3, \ x=1; \
xin[1;3].](https://tex.z-dn.net/?f=f%28x%29%3D25%2C+3%5E%7Bx%7D-2%3D25%2C+%5C%0A+3%5E%7Bx%7D%3D27%2C+%5C++3%5E%7Bx%7D%3D3%5E3%2C+%5C+x%3D3%3B+%5C%0Af%28x%29%3D1%2C+3%5E%7Bx%7D-2%3D1%2C+%5C%0A+3%5E%7Bx%7D%3D3%2C+%5C++x%3D1%3B+%5C%0Axin%5B1%3B3%5D.%0A "f(x)=25, 3^{x}-2=25, \
3^{x}=27, \ 3^{x}=3^3, \ x=3; \
f(x)=1, 3^{x}-2=1, \
3^{x}=3, \ x=1; \
xin[1;3].")
3.
2.
3.
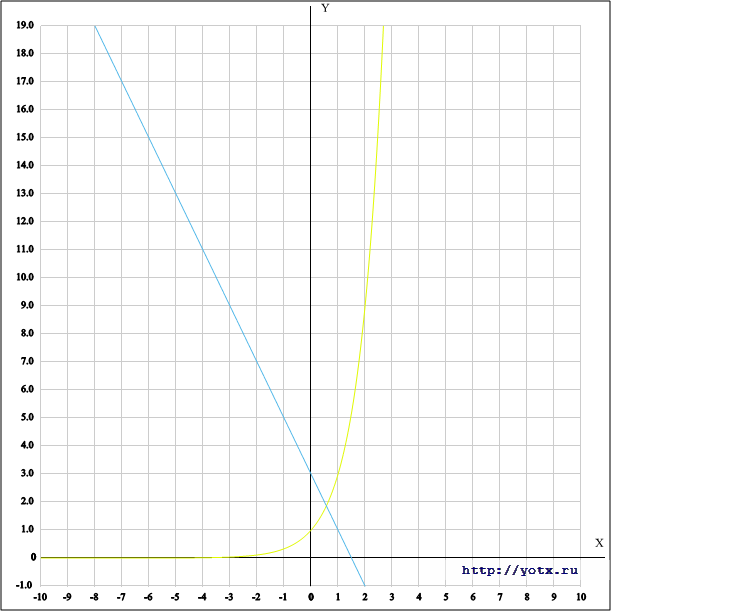
Приложения:
Похожие вопросы
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад