Внешний угол прямоугольного
треугольника в 2 раза больше угла,
смежного с ним. Найдите меньший отрезок
гипотенузы, который отсекает
перпендикуляр, проведённый из вершины
прямого угла на гипотенузу, если
гипотенуза равна 100.
Ответы
Ответ дал:
0
Внешний угол прямоугольного треугольника в 2 раза больше угла, смежного с ним. Найдите меньший отрезок гипотенузы, который отсекает перпендикуляр, проведённый из вершины прямого угла на гипотенузу, если гипотенуза равна 100.
——
Внешний угол и смежный с ним составляют развернутый угол, величина которого, как известно, равна 180°
Пусть данный угол треугольника будет х°, а внешний 2х°
Тогда сумму этих углов можно записать уравнением
х+2х=180°
3х=180°х=60°
Сумма острых углов прямоугольного треугольника равна 90°
⇒ второй острый угол равен 30°
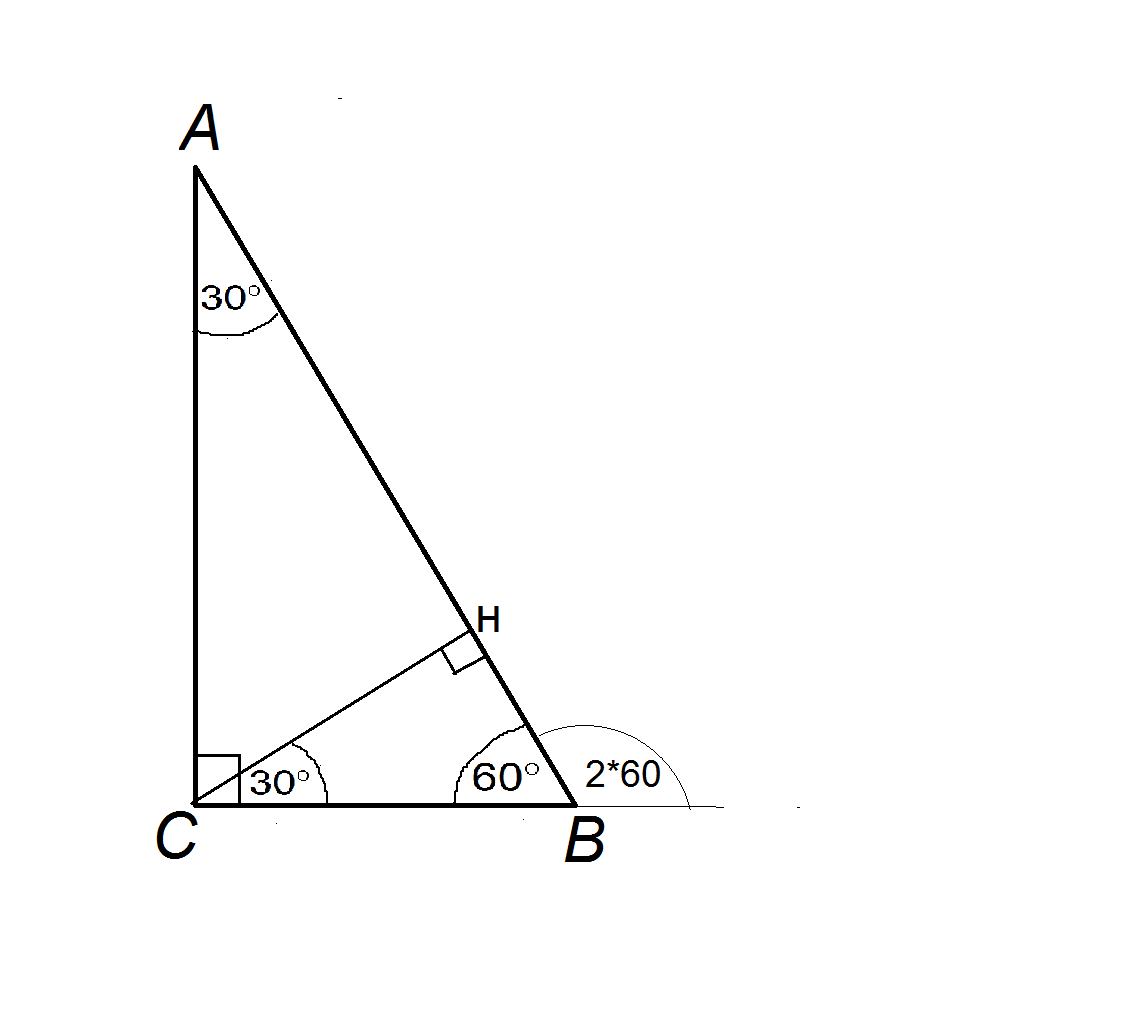
Меньший катет ( на рисунке это катет СВ) противолежит углу 30° и равен половине гипотенузы.
СВ=100:2=50
Перпендикуляр, проведённый из вершины прямого угла на гипотенузу, делит ее на два отрезка. Меньший - НВ- прилежит углу 60° и противолежит углу 30°
НВ=СВ:2
НВ=50:2=25
——
Внешний угол и смежный с ним составляют развернутый угол, величина которого, как известно, равна 180°
Пусть данный угол треугольника будет х°, а внешний 2х°
Тогда сумму этих углов можно записать уравнением
х+2х=180°
3х=180°х=60°
Сумма острых углов прямоугольного треугольника равна 90°
⇒ второй острый угол равен 30°
Меньший катет ( на рисунке это катет СВ) противолежит углу 30° и равен половине гипотенузы.
СВ=100:2=50
Перпендикуляр, проведённый из вершины прямого угла на гипотенузу, делит ее на два отрезка. Меньший - НВ- прилежит углу 60° и противолежит углу 30°
НВ=СВ:2
НВ=50:2=25
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад