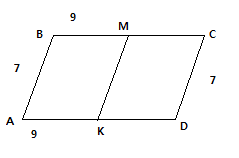
В параллелограмме ABCD на сторонах BC и AD взяты соответственно точки М и К-середины этих сторон. Определите вид четырёхугольника ABMK(ОТВЕТ ОБОСНУЙТЕ) и найдите его периметр если AB=7 см, BC=9 см.

Рисунок в прикрепленном файле. 

Так как М середина ВС, то ВМ=МС=9:2=4,5 см
Ан-но, К - середина AD, AK=KD=9:2=4,5 см
Получили, что ВМ=AK=4,5 см, ВМ || AK

Зная, что АВСD параллелограмм, АВ=CD=7=MK, потому как ВМ=AK=4,5 см равные отрезки содержатся между параллельными прямыми/сторонами.
Получили, что АВMK - параллелограмм.

Р=2*(4,5+7)=2*11,5=23 см.