Предмет: Алгебра
Автор: ivan733
Вопрос задан 9 лет назад

вычислить площадь фигуры, ограниченной линиями x-2y+4=0, x+y-5=0, y=0

Ответы

Ответ дал: nafanya2014

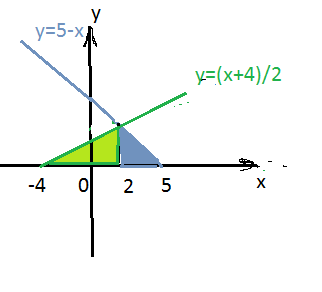
Находим точку пересечения прямых x-2y+4=0, x+y-5=0:
$left { {{x-2y+4=0} atop {x+y-5=0}} right.$
Вычитаем из первого уравнения второе:
-2у-у+4+5=0
-3у=- 9
у= 3 ⇒ х = 5 - у= 5 - 3=2
Прямая x-2y+4=0 пересекает ось ох в точке у=0, х=-4
Прямая x+y-5=0 пересекает ось ох в точке у=0, х=5
$S= intlimits^2_{-4} { frac{x+4}{2} } , dx + intlimits^5_2 { (5-x) } , dx= (frac{ x^{2} }{4}+2x)| _{-4} ^{2} +(5x- frac{ x^{2} }{2})| _{2} ^{5}= \ =(1+4)-(4-8)+(25- frac{25}{2})-(10-2)=5+4+12,5-8=13,5$
Проверка:
Площадь первого прямоугольного треугольника равна половине произведения катетов
6·3/2=9 кв. ед.
Площадь второго прямоугольного треугольника равна половине произведения катетов
3·3/2=4,5 кв. ед.
Сумма площадей
9+4,5=13,5 кв. ед

Приложения: