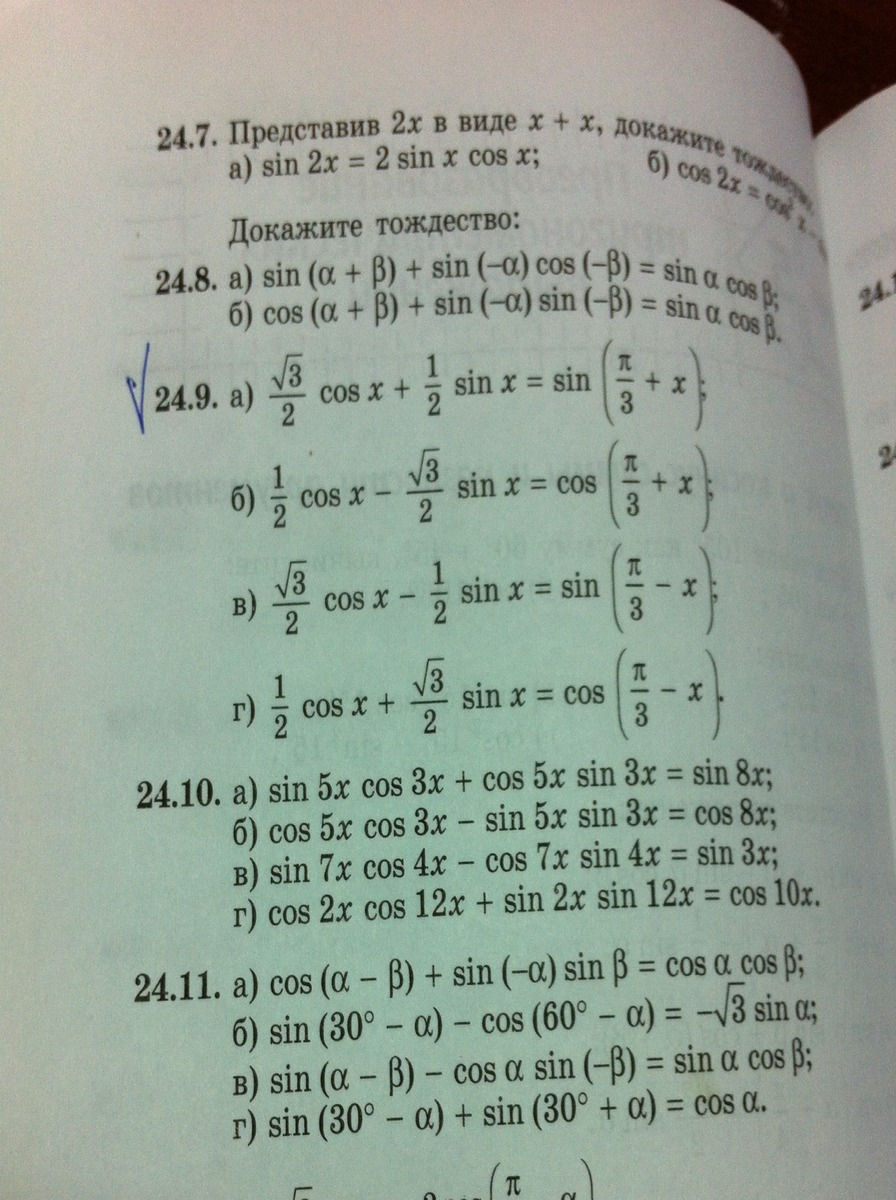Ответы
Ответ дал:
0
Решение
Учитывая, что sin(π/3) = √3/2; cos(π/3) = 1/2 и применяя формулы сложения и вычитания, получаем:
1) sin(π/3)*sinx + cos(π/3)*cosx = sin(π/3 + x)
2) cos(π/3)*cosx - sin(π/3)*sinx = cos(π/3 + x)
3) sin(π/3)*cosx - cos(π/3)*sinx = sin(π/3 - x)
4) cos(π/3)*cosx + sin(π/3)*sinx = cos(π/3 - x)
Учитывая, что sin(π/3) = √3/2; cos(π/3) = 1/2 и применяя формулы сложения и вычитания, получаем:
1) sin(π/3)*sinx + cos(π/3)*cosx = sin(π/3 + x)
2) cos(π/3)*cosx - sin(π/3)*sinx = cos(π/3 + x)
3) sin(π/3)*cosx - cos(π/3)*sinx = sin(π/3 - x)
4) cos(π/3)*cosx + sin(π/3)*sinx = cos(π/3 - x)
Похожие вопросы
2 года назад
7 лет назад
10 лет назад
10 лет назад