докажите, что если бессектриса треугольника является его высотой, то этот треугольник равнобедренный

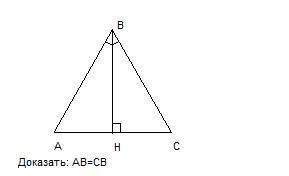
По условию ВН также - высота. Имеется два прямоугольных треугольника АНВ и СНВ. Они равны по одному из признаков равенства прямоугольных треугольников: катет и прилежащий к нему острый угол одного прямоугольного треуг-ка соответственно равны катету и прилежащему к нему острому углу другого. В нашем случае:
ВН - общий катет;
<ABH=<CBH, т.к. ВН по условию - биссектриса.
У равных треугольников соответственные стороны равны, т.е. АВ=СВ, значит, АВС - равнобедренный.