• Предмет: Математика
  • Автор: arshatik001
  • Вопрос задан 9 лет назад
< >

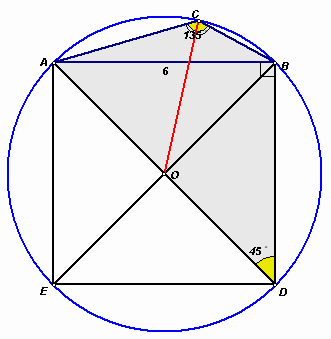
В треугольнике АВС угол С равен 135 градусов. На стороне АВ вне треугольника построен квадрат с центром О. Найдите ОС, если АВ=6

Ответы

Ответ дал: himach
0
Решение: Пусть АВDE – построенный квадрат. Его диагональ образует со стороной угол 45°, значит,  ∠ACB + ∠ADB = 180°  (см. рис.). Следовательно, около четырёхугольника ACBD можно описать окружность. Так как угол ABD, вписанный в эту окружность, прямой, то центр О окружности является серединой диагонали AD квадрата, то есть его центром. Тогда ОС – радиус этой окружности. Таким образом, OC =  frac{1}{2} AD=3 sqrt{2}

Ответ: 3√2
Приложения:
Ответ дал: nafanya2014
0
Надо найти этот радиус ОС. Чему же он равен?
Ответ дал: nafanya2014
0
О-центр окружности описанной около квадрата. Почему точка С лежит на этой окружности?.
Ответ дал: himach
0
треугольник
Похожие вопросы
Русский язык
2 года назад
чем отличаются согласованные определения от несогласованны,приведите примеры
Русский язык
2 года назад
как проверить слово целина
Физика
7 лет назад
Можно пожалуйста решение этого
Геометрия
7 лет назад
Известны стороны равнобедренного треугольника 2 см и 5 см. Чему равен его периметр? Решите с рисунком и дано. Пожалуйста очень надо!
Биология
10 лет назад
напишите доклад на тему: почему вымерли динозавры?
Физика
10 лет назад
В цепи, изображенной на рисунке, ползунок реостата перемещают вниз. Как изменились показания амперметра и вольтметра? а) Показания обоих приборов увеличились. б) Показания обоих приборов уменьшились.
Алгебра
10 лет назад
ребята, дайте сложненькие задачки по математике 7 класс на составление СИСТЕМ уравнений)плизик)хоть 1-2)на движение, если можно)или на концентрацию со сплавами)
Алгебра
10 лет назад
Найдите корень уравнения 4^-5+x=64