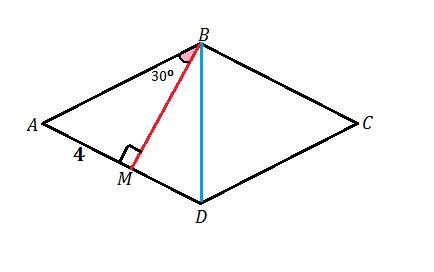
Высота ВМ, проведенная из вершины угла ромба АВСД образует со стороной АВ угол 30 градусов , АМ=4см.Найдите длину диагоналей ВД , если точка М лежит на стороне АД

Высота ВМ  отсекает от ромба прямоугольный треугольник АВМ. Катет АМ противолежит углу 30º и равен половине гипотенузы АВ.
АВ=4*2=8 см
Сумма острых углов прямоугольного треугольника равна 90.
Т.к. угол АВМ=30º, угол ВАD=90-30=60
Все стороны ромба равны. ⇒АD=AB, треугольник ВАD равнобедренный с углом при А=60 ⇒угол АВD= углу ADB=(180-60):2=60
Треугольник АВD  равносторонний, BD=AB=AD=8 cм.
Диагональ ВD=8 см