Ответы
Ответ дал:
0
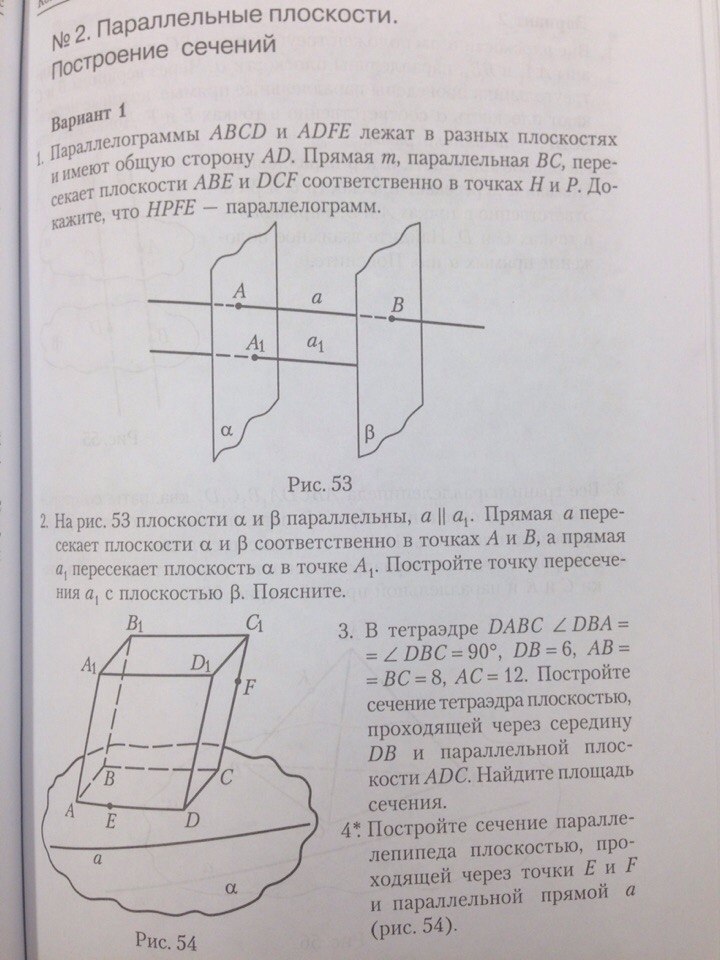
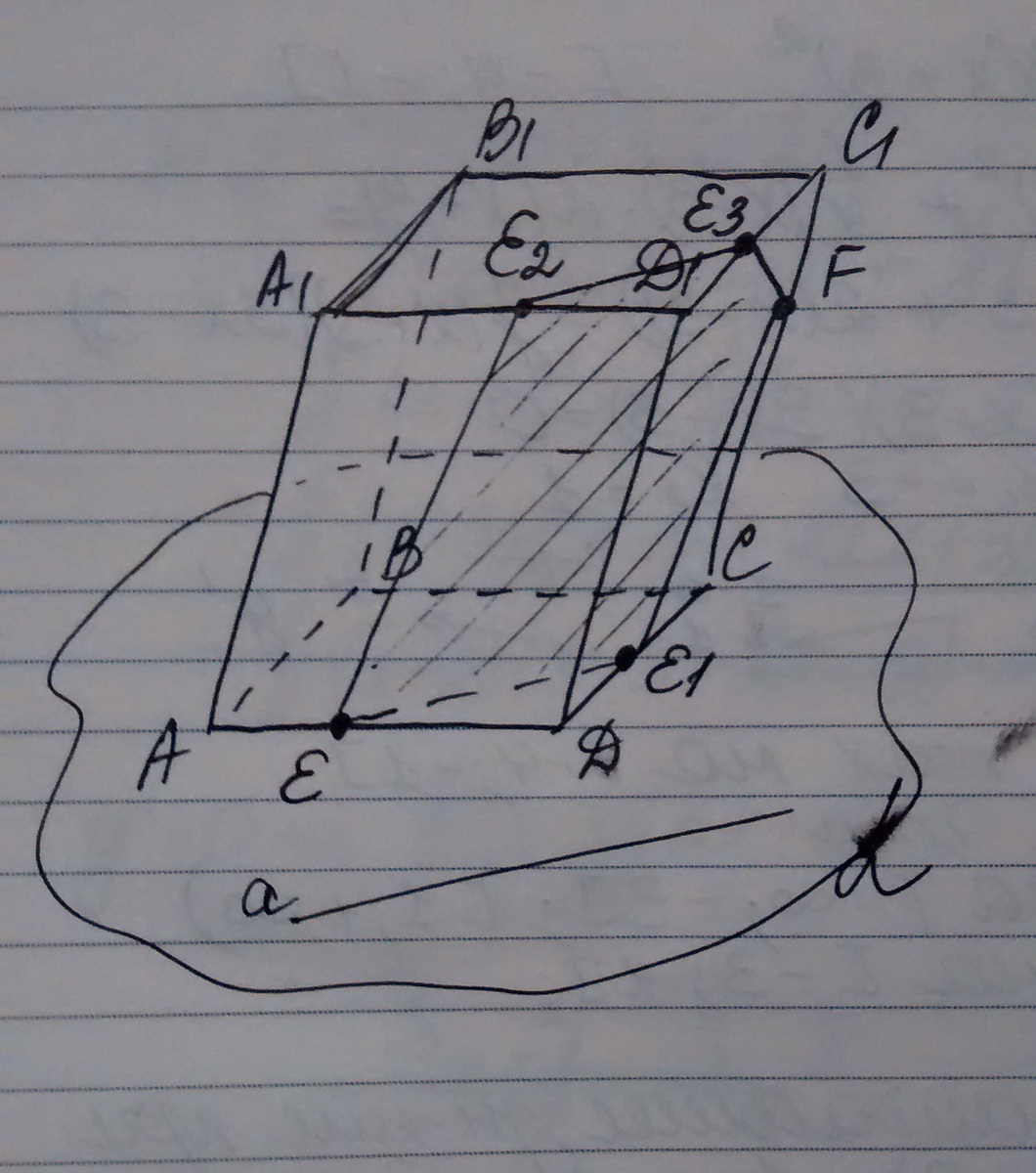
Через точку Е проведем ЕЕ1 прямую, параллельную прямой а.
Точки Е1 и F принадлежат одной плоскости, следовательно, соединим Е1 и F.
В плоскости АА1D1 проведем прямую ЕЕ2, параллельную Е1F.
В плоскости А1B1C1 через Е2 проведем Е2Е3 || EE1 || a.
Е3 и F принадлежат одной плоскости DD1C1, следовательно, соединим Е3 и F.
Итого, получили сечение EE1FE3E2 параллелепипеда ABCDA1B1C1D1.
Точки Е1 и F принадлежат одной плоскости, следовательно, соединим Е1 и F.
В плоскости АА1D1 проведем прямую ЕЕ2, параллельную Е1F.
В плоскости А1B1C1 через Е2 проведем Е2Е3 || EE1 || a.
Е3 и F принадлежат одной плоскости DD1C1, следовательно, соединим Е3 и F.
Итого, получили сечение EE1FE3E2 параллелепипеда ABCDA1B1C1D1.
Приложения:
Ответ дал:
0
+)
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад