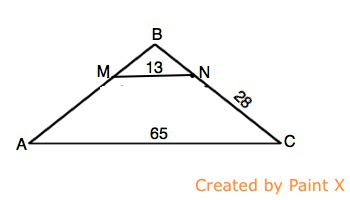
Прямая параллельная стороне ас треугольника авс пересекает стороны ав и вс в точках m и n соответственно.найдите bn если mn=13 ac=65 nc=28
Ответы
Ответ дал:
0
MN||АС; В ∆ АВС и ∆ MBN угол В - общий, ∠ВNM=∠BCA и ∠BMN=∠BAC как соответственные при пересечении параллельных прямых секущей. ⇒
∆ АВС и ∆ MBN подобны.
Коэффициент подобия AC:MN=65:13=5:1⇒
ВС: BN=5:1
BN- 1 часть, CN=4 части.
28:4=7=длина 1 части.
ВN=7 (ед. длины)
----------------
ВС=BN+MC=7+28=35
BC:BN=35:7=5:1
Приложения:
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад