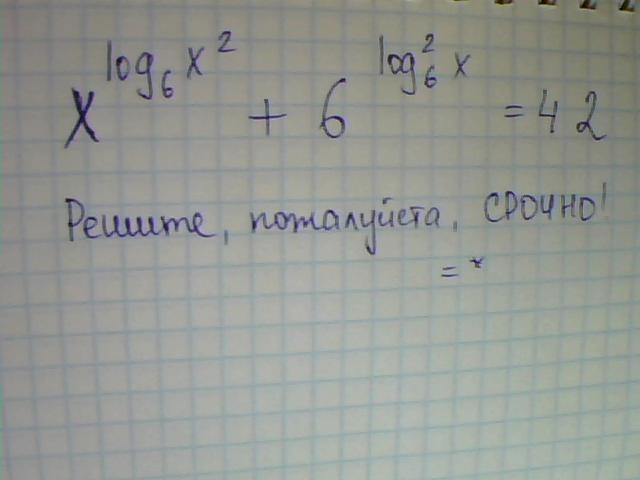Ответы
Ответ дал:
0
По свойству степени
Тогда исходное уравнение принимает вид
![x^{log_6x^2}+x^{log_6x}=42 \
x^{2log_6x}+x^{log_6x}=42 \
(x^{log_6x})^2+x^{log_6x}=42](https://tex.z-dn.net/?f=x%5E%7Blog_6x%5E2%7D%2Bx%5E%7Blog_6x%7D%3D42+%5C+%0Ax%5E%7B2log_6x%7D%2Bx%5E%7Blog_6x%7D%3D42+%5C+%0A%28x%5E%7Blog_6x%7D%29%5E2%2Bx%5E%7Blog_6x%7D%3D42 "x^{log_6x^2}+x^{log_6x}=42 \
x^{2log_6x}+x^{log_6x}=42 \
(x^{log_6x})^2+x^{log_6x}=42")
Обозначим
Получается квадратное уравнение относительно у
![y^2+y=42 \ y^2+y-42=0 \
D=1^2-4*(-42)=169 \
sqrt{D} =13 \
y_1=(-1-13)/2=-7 \
y_2=(-1+13)/2=6](https://tex.z-dn.net/?f=y%5E2%2By%3D42+%5C+y%5E2%2By-42%3D0+%5C+%0AD%3D1%5E2-4%2A%28-42%29%3D169+%5C+%0A+sqrt%7BD%7D+%3D13+%5C+%0Ay_1%3D%28-1-13%29%2F2%3D-7+%5C+%0Ay_2%3D%28-1%2B13%29%2F2%3D6 "y^2+y=42 \ y^2+y-42=0 \
D=1^2-4*(-42)=169 \
sqrt{D} =13 \
y_1=(-1-13)/2=-7 \
y_2=(-1+13)/2=6")
Возвращаемся к переменной х
Решений нет
Логарифмируем
![log_6(x^{log_6x})=log_66 \
log_6x*log_6x=1 \
(log_6x)^2=1 \
log_6x=б1 \
x_1=6^{-1}= frac{1}{6} \
x_2=6^1=6](https://tex.z-dn.net/?f=log_6%28x%5E%7Blog_6x%7D%29%3Dlog_66++%5C+%0Alog_6x%2Alog_6x%3D1+%5C+%0A%28log_6x%29%5E2%3D1+%5C+%0Alog_6x%3D%D0%B11+%5C+%0Ax_1%3D6%5E%7B-1%7D%3D+frac%7B1%7D%7B6%7D++%5C+%0Ax_2%3D6%5E1%3D6 "log_6(x^{log_6x})=log_66 \
log_6x*log_6x=1 \
(log_6x)^2=1 \
log_6x=б1 \
x_1=6^{-1}= frac{1}{6} \
x_2=6^1=6")
Ответ:
Тогда исходное уравнение принимает вид
Обозначим
Получается квадратное уравнение относительно у
Возвращаемся к переменной х
Решений нет
Логарифмируем
Ответ:
Ответ дал:
0
Спасибо!)
Ответ дал:
0
Пожалуйста)
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад