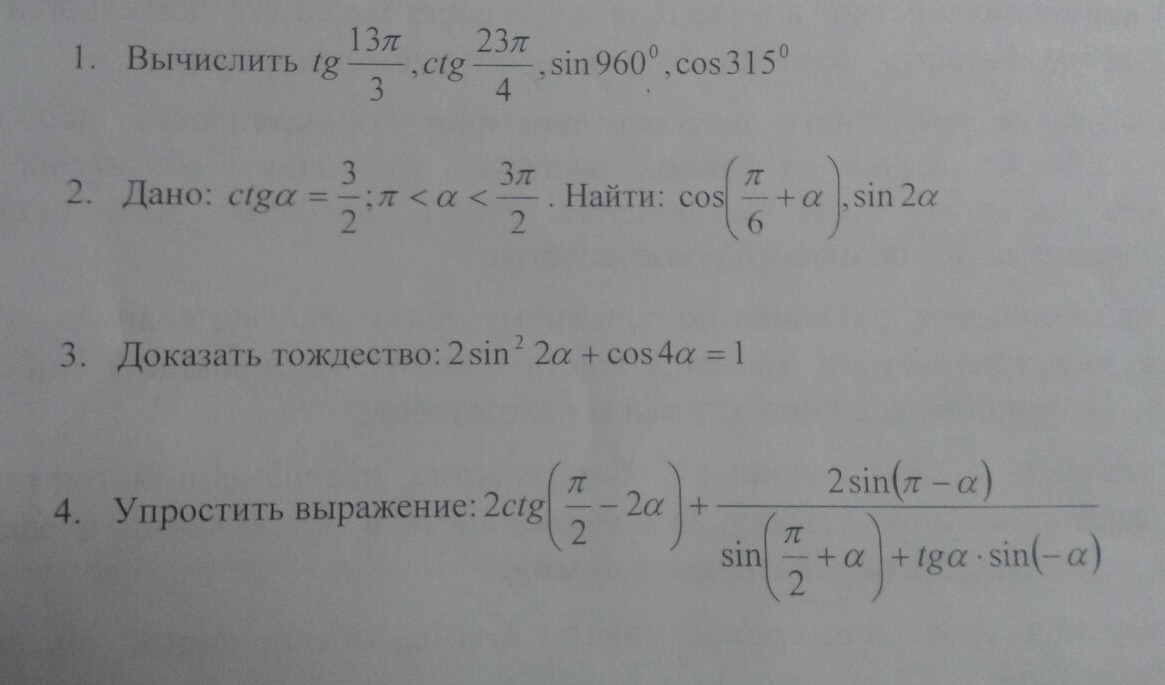Ответы
Ответ дал:
0
1)

3)

4)

2)

α∈(π;3π/2)⇒угол 3 четверти⇒sinα и cosα отрицательны(перед корнем буду стоять минус.


Во вложении формулы приведения.
3)
4)
2)
α∈(π;3π/2)⇒угол 3 четверти⇒sinα и cosα отрицательны(перед корнем буду стоять минус.
Во вложении формулы приведения.
Приложения:

Похожие вопросы
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад