Отрезок ВС-диаметр окружности.Прямая АВ касательная к окружности а прямая АС пересекает окружность в точке Д.Вычислите градусные меры треугольник ВАД если известно что дуга ВД=120 градусов.

Применим способ нахождения углов:
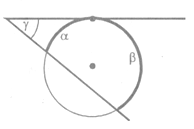
Если из точки, лежащей вне круга, проведены секущая и касательная, то
γ = (β – α)/2  (Смотри рисунок)

Здесь угол А-γ
Применив это правило, находим угол А=(180-120):2=30°
Так как треугольник АВД прямоугольный ( диаметр ВД и касательная АВ пересекаются под прямым углом), угол АВД=90°,

угол ВДА, соответственно, 90-30=60°.

∠А=(180-120):2=30°

∠АВД=90°

∠ВДА=60°