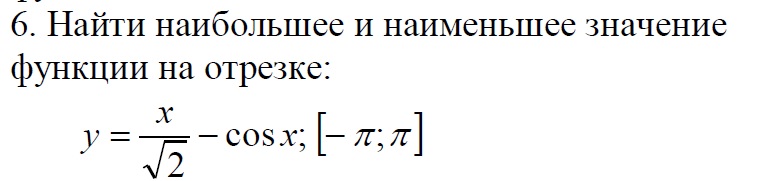Ответы
Ответ дал:
0
y = x/√2 - cosx [-π;π]
Находим первую производную функции:
y! = sinx + (1/2)√2
Приравниваем ее к нулю:
sinx + (1/2)√2 = 0
x1 = -(π/4)
Вычисляем значения функции на концах отрезка
f(-π/4) = (1/8)*√2*(- 4 - π)
f(-π) = -1.2214
f(π) = 3.2214
Ответ: fmin = (1/8)*√2*(- 4 - π) ; fmax = 3,22
Находим первую производную функции:
y! = sinx + (1/2)√2
Приравниваем ее к нулю:
sinx + (1/2)√2 = 0
x1 = -(π/4)
Вычисляем значения функции на концах отрезка
f(-π/4) = (1/8)*√2*(- 4 - π)
f(-π) = -1.2214
f(π) = 3.2214
Ответ: fmin = (1/8)*√2*(- 4 - π) ; fmax = 3,22
Ответ дал:
0
Спасибо ,тебе огромное
Ответ дал:
0
только эта точка ,больше никаких нет?я про x1
Ответ дал:
0
просто я переделываю задание ,там написано еще точки
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад