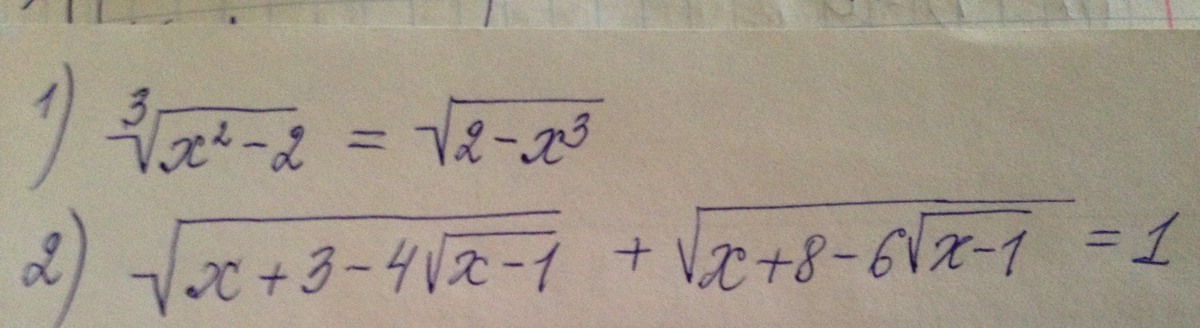Предмет: Алгебра
Автор: yurl201032
Вопрос задан 9 лет назад

Требуется решение. Заранее благодарю

Приложения:

Ответы

Ответ дал: Аноним

$sqrt[3]{x^2-2} = sqrt{2-x^3}$
Отметим ОДЗ:
$2-x^3 geq 0 \ x leq sqrt[3]{2}$
ПРоизведем замену
$left { {{a= sqrt{2-x^3} } atop {b= sqrt[3]{x^2-2} }} atop {b-a=0}right.$
Если $a= sqrt{2-x^3}$ , то в итоге получаем $a^2=2-x^3$
Аналогично $sqrt[3]{x^2-2}=b to x^2-2=b^3$
Из уравнение b-a=0, выразим переменную b тоесть a=b.
$left { {{-x^3+2-a^2=0} atop {x^2-2-a^3=0}} right. to left { {{(-x^3+2-a^2)+(x^2-2-a^3)=0} atop {x^2-2-a^3=0}} right.$
$-x^3-a^2+x^2-a^3=0 \ (-a^2+ax-x^2)(a+x)-(a-x)(a+x)=0 \ (a+x)(-a^2+ax-x^2-a+x)=0$
Решаем 2 уравнения
$-a^2+ax-x^2-a+x=0 \ (-a^2+ax-x^2-a+x)+(x^2-2-a^3)=0 \ -a^2+ax-a+x-2-a^3=0 \ (a+1)x-a^2-a-2-a^3=0 \ x= frac{a^2+a+2+a^3}{a+1} ;,,, a+1neq 1$
В ОДЗ подставим вместо х
$frac{a^2+a+2+a^3}{a+1} leq sqrt[3]{2}$
$a^3+a^2-(-1+ sqrt[3]{2} )a+(2- sqrt[3]{2} ) leq 0$
Получаем левую часть положительный значением. Значит неравенство решений не имеет.
Второе уравнение a+1=0
a=-1 - подставим
$left { {{(-1)^2+(-1)+2+(-1)^3=0} atop {x&2-2-(-1)^3=0}} atop {-1 geq 0}right. toO$

Итак, уравнение решений не имеет.

Ответ: нет решений.

$sqrt{x+3-4 sqrt{x-1}} + sqrt{x+8-6 sqrt{x-1} } =1 \$

Отметим ОДЗ:

$left { {{x+8-6 sqrt{x-1} geq 0 } atop {x-1 geq 0}}atop {x+3-4 sqrt{x-1} geq 0 } right.$

Пусть $sqrt{x-1}=a (a geq 0),$ тогда имеем x=a^2+1
$(x+3-4a)^{ frac{1}{2} }+(x+8-6a)^{ frac{1}{2} }=1 \ x+8-6a=1-2(x+3-4a)^{ frac{1}{2} }+(x+3-4a) \ a-2=(x+3-4a)^{ frac{1}{2} } \ a^2-4a+4=x+3-4a \ \ a^2-4a+1=a^2+1+3-4a \ 0=3$

Ответ: $x=a^2+1$ при $a in [2;3]$