Предмет: Физика
Автор: DmitrPowerPlay
Вопрос задан 9 лет назад

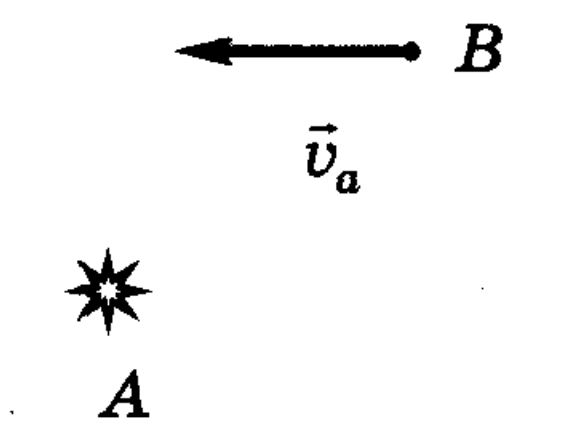
В некоторой точке A в стороне от шоссе находится человек.На шоссе в точке B человек увидел автобус, движущийся со скоростью Vа. С какой минимальной скоростью должен бежать человек к шоссе, чтобы успеть сесть в автобус? В каком направлении он должен бежать? Задачу решите графически.

Приложения:

Ответы

Ответ дал: Zixel

Значит действуем следующим образом.
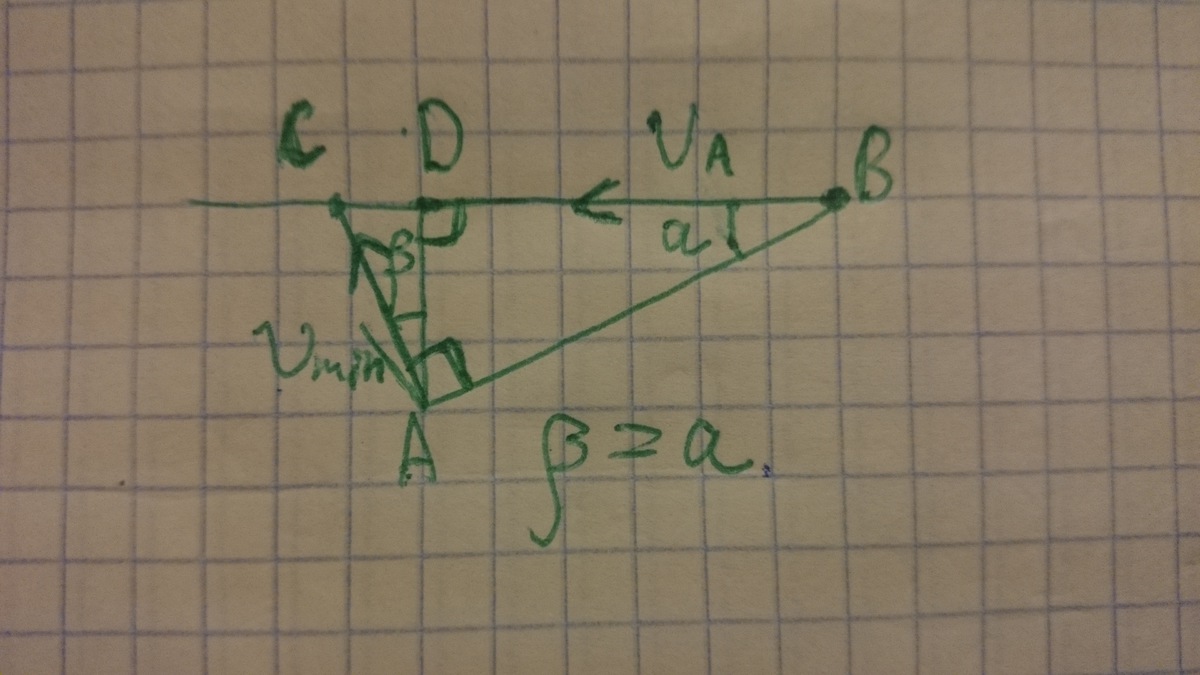
Очевидно, что он должен бежать за перпендикуляр к дороге, а не перед ним(тогда у него будет больше времени, значит, его скорость будет меньше:)).
Итак, пусть расстояние вдоль дороги, которое ему надо пробежать вдоль дороги(также расстояние от места встречи с автобусом до перпендикуляра к дороге) равно x.
Также обозначим за L расстояние от перпендикуляра до автобуса, а d - расстояние до дороги от путника(перпендикуляр). И обозначим время до встречи за t. Итак, t = (x + L)/Vа (время, за которое автобус доедет до места встречи). Также скорость путника v равна $v = (sqrt{ x^{2} + d^{2} }) /t$ Подставим t из первого уравнения: $v = (sqrt{ x^{2} + d^{2} }*Va) /(x+L)$ . Мы получили функцию скорости v от x. Беря производную этого выражения получаем минимум функции v(x). Этот минимум - и есть минимальная скорость. Берем производную: $v'(x) = Va*((x+L)'( sqrt{x^{2} + d^{2} } ) - (x+L)( sqrt{x^{2} + d^{2} } )')/ (x+L)^{2}$ $=Va( sqrt{ x^{2} + d^{2} }-x(L+x) /sqrt{ x^{2} + d^{2} })/(x+L)^2$ .
Отлично, половина работы сделана. Приравняем производную к нулю, чтобы получить минимум: $Va( sqrt{ x^{2} + d^{2} }-x(L+x) /sqrt{ x^{2} + d^{2} })/(x+L)^2 = 0$ , => $x^{2} + d^{2} - x(x+L) = 0=> x = d^{2} /L.$ $d/L = tg( alpha )$ (пояснение в рисунке) => $x = d*tg( alpha )$ ; $x/d = tg( beta ) = tg( alpha )=> beta = alpha$ , значит человек должен взять направление, идущее под углом (90-a) к дороге. Ну и подставим x в уравнение скорости пешехода для нахождения оной)))
$vmin = sqrt{ x^{2}+ d^{2} } *Va/(x+L) = Va*dL sqrt{ (d/L)^{2} + 1 } /( d^{2} + L^{2} )$
Upd: С телефона решительно невозможно что-либо отправить! Браузерный интерфейс этого сайта нереально убог! Пришлось искать кабель, чтобы перекинуть фотку, с телефона так и не удалось.

Приложения: