высота правильной треугольной пирамиды равна 16, а высота её основания равна 6. Найдите тангенс угла между плоскостью боковой грани и плоскостью основания.

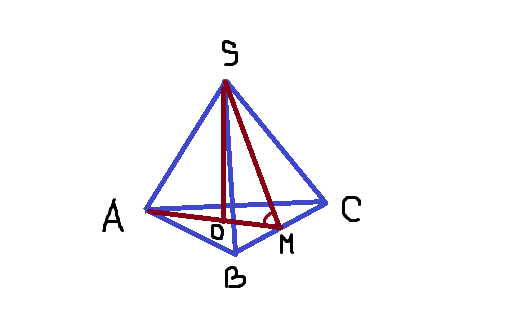
ОМ=1/3АМ=2 (т.к. высота пирамиды падает в центр вписанной и описанной окружности - точка пересечения биссектрис и медиан и высот так как треугольник правильный,и медианы пересекаются в одной точке и точкой пересечения делятся в отношении 2:1 считая от вершины)
из прямоуг треуг SOM tg угла между плоскостью основания и высотой равен SO/OM=16/2=8