дано вот такое уравнение.надо его решить на интервале от 1 до 2 включительно.ответ П/2
Приложения:
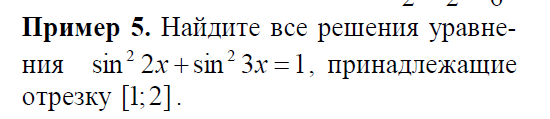
Ответы
Ответ дал:
0
Формула понижения степени:

Уравнение принимает вид

или
cos 4x+cos 6x=0
Формула

2cos5x·cos(-x)=0
cos x=0 или cos 5x=0
x=π/2 + πk,k∈Z или 5x=π/2 + πn, n∈Z
х=π/10+(π/5)n, n∈Z
π/2∈[1;2]
Уравнение принимает вид
или
cos 4x+cos 6x=0
Формула
2cos5x·cos(-x)=0
cos x=0 или cos 5x=0
x=π/2 + πk,k∈Z или 5x=π/2 + πn, n∈Z
х=π/10+(π/5)n, n∈Z
π/2∈[1;2]
Ответ дал:
0
а почему второй корень не подходит?
Ответ дал:
0
Потому что при n=0 получаем π/10 это приближенно 0,3 <1. При n=1 получаем π/10+π/5=3π/10, приближенно 0,9<1 При n=2 получаем π/10+(2π/5)=π/2 При n=3 получаем π/10+(3π/5)=7π/10>2
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад