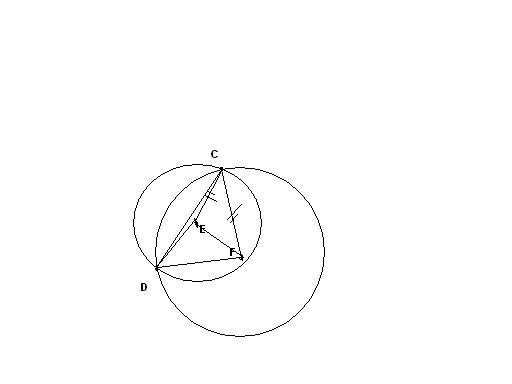
Окружности с центрами в точках Е и F
пересекаются в точках С и D причем
точки Е и F лежат по одну сторону от
прямой СD.Докажите что СD
перпендикулярна EF и рисунок
Ответы
Ответ дал:
0
Рассматриваем треугольник(его рисовать не обязательно) ECD.В нём
EC=CD(след-но, треугольник равнобедренный) .Нужно доказать,что EF перпендикулярена CD.Для этого строим FC
и FD,опять равнобедренный треугольник FCD,где FC=FD.Из равенства углов
ECD=CDE и FCD=FDC получаем,что ECK=KDE. Треугольники ECF и EDF
равны по двум сторонам и двум углам между ними.Поэтому,
угол CEK=DEK.
Теперь вернёмся к треугольнику ECF.В нём EF-биссектрисса,а значит и медиана.Отсюда следует,что EF=CD.Теорема доказана.
Теперь вернёмся к треугольнику ECF.В нём EF-биссектрисса,а значит и медиана.Отсюда следует,что EF=CD.Теорема доказана.
Приложения:
Ответ дал:
0
спасибо
Ответ дал:
0
не за что)
Похожие вопросы
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад