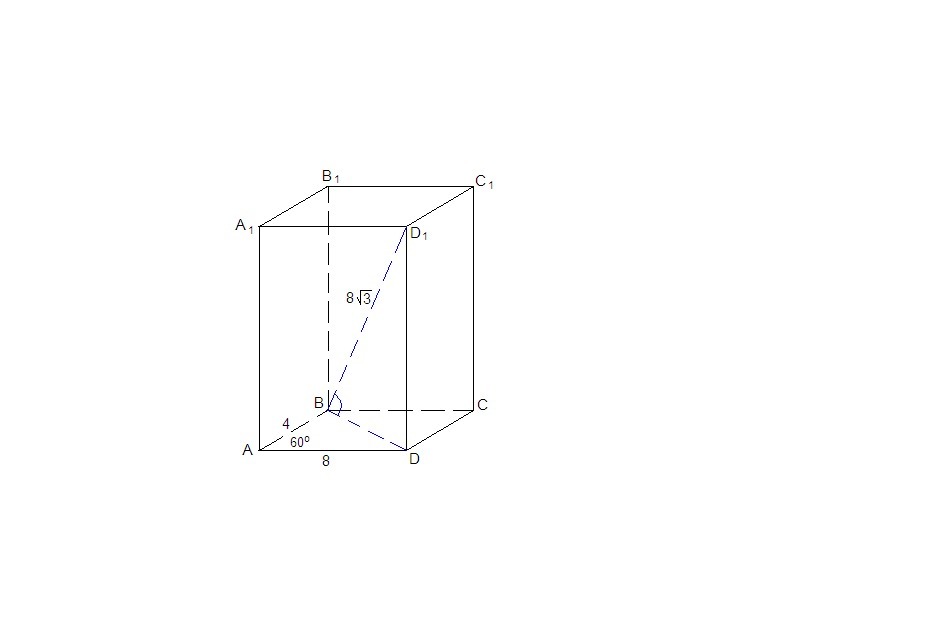
в прямом параллелепипеде стороны основания равны 8 и 4 и составляют угол в 60градусов. Меньшая диагональ параллелепипеда 8корень3. Какой угол составляет эта диагональ с плоскостью основания?

Параллелепипед прямой, значит боковые ребра перпендикулярны основанию.
BD - проекция диагонали BD₁ на плоскость основания, тогда
∠D₁BD - искомый.

Из треугольника ABD по теореме косинусов:
BD² = AB² + AD² - 2AB·AD·cos60°
BD² = 16 + 64 - 2 · 4 · 8 · 1/2 = 80 - 32 = 48
BD = 4√3

ΔD₁BD: ∠D₁DB = 90°
               cos∠D₁BD = BD/D₁B = 4√3 / (8√3) = 1/2
               ∠D₁BD = 60°