Докажите, что биссектрисы равных треугольников,проведенные из соответствующих углов этих треугольников ,равны между собой.

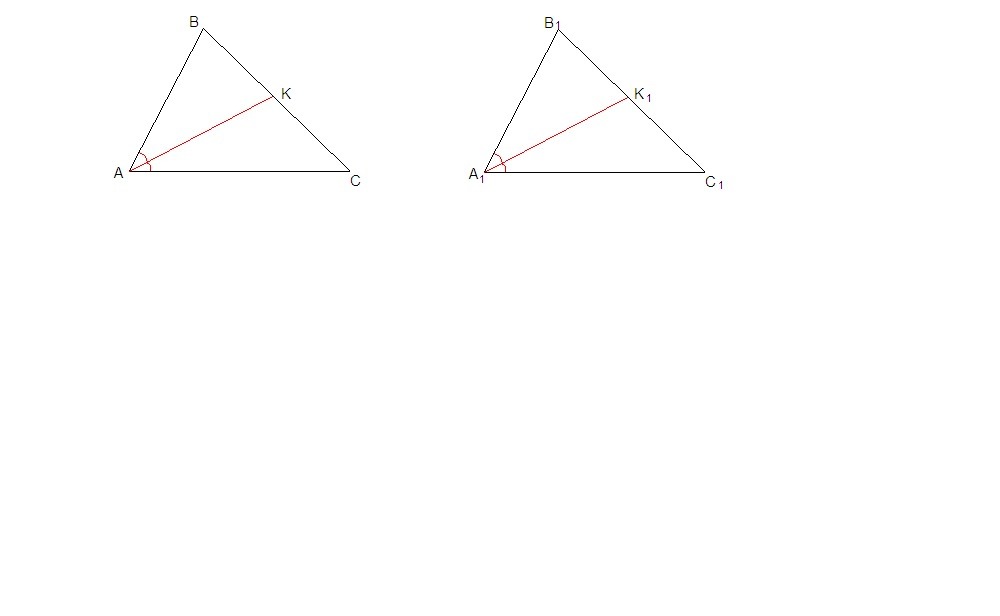
Пусть ΔАВС = ΔА₁В₁С₁, надо доказать, что биссектрисы равных углов равны, т.е. что АК = А₁К₁.

АС = А₁С₁ из равенства треугольников,
∠КСА = ∠К₁С₁А₁ из равенства треугольников,
∠КАС = ∠К₁А₁С₁ как половины равных углов,
значит ΔАКС = ΔА₁К₁С₁ по стороне и двум прилежащим к ней углам, следовательно и АК = А₁К₁ как стороны равных треугольников, лежащие напротив равных углов.