В выпуклом четырехугольнике диагонали взаимно перпендикулярны.Докажите, что S четырехугольника равна половине произведения его диагоналей.

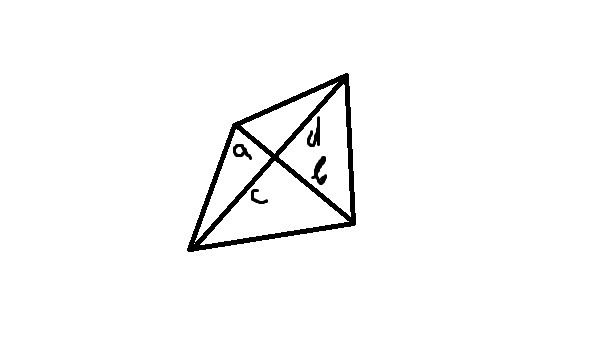
Обозначим части диагоналей буквами a, b, c, d как показано на рисунке. Общая площадь фигуры будет складываться из площадей четырех прямоугольных треугольников. 

ч.т.д.