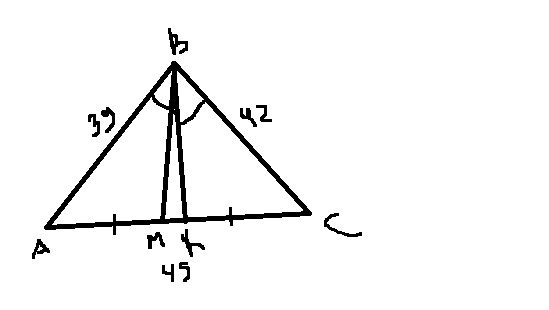
В треугольнике АВС АВ = 39, ВС = 42, СА = 45. Найдите площадь треугольника, образованного стороной АС, биссектрисой ВК и медианной ВМ.

площадь АВС=√63*21*24*18=√9*7*7*3*3*8*9*2=3*7*3*3*4=756
площадь АВМ = площади ВСМ = 1/2АВС=378 т.к. если высоты одинаковые то площади относятся как основания, а основания равны, потому что ВМ - медиана
площадь АВК=1/2*АВ*ВК*sin(B/2)
площадь CВК=1/2*CВ*ВК*sin(B/2) эти площади относятся как 39/42,, тогда
S(ABK)=39/81S(ABC)=39*756/81=364
S(BKM)=378-364=14

Спасибо есть же добрые люди))