Предмет: Геометрия
Автор: Аноним
Вопрос задан 10 лет назад

В треугольнике ABC углы A и C соответственно равны альфа и бета. AD - биссектриса треугольника. Найти площадь треугольника ADC,если AD=n.

Ответы

Ответ дал: dtnth

угол А=альфа, угол С=бэта,

значит угол CAD=альфа/2

угол ADC=180-угол CAD-угол C

по формуле площади треугольника за данной одной стороной и углами

$S(ADC)=frac{AD^2 *sin (CAD)*sin (ADC)}{2sin C}=\ frac{n^2 sin frac{alpha}{2}sin (180-beta-frac{alpha}{2})}{2sinbeta}=\ frac{n^2 sin frac{alpha}{2}sin (beta+frac{alpha}{2})}{2sinbeta}$

Приложения:

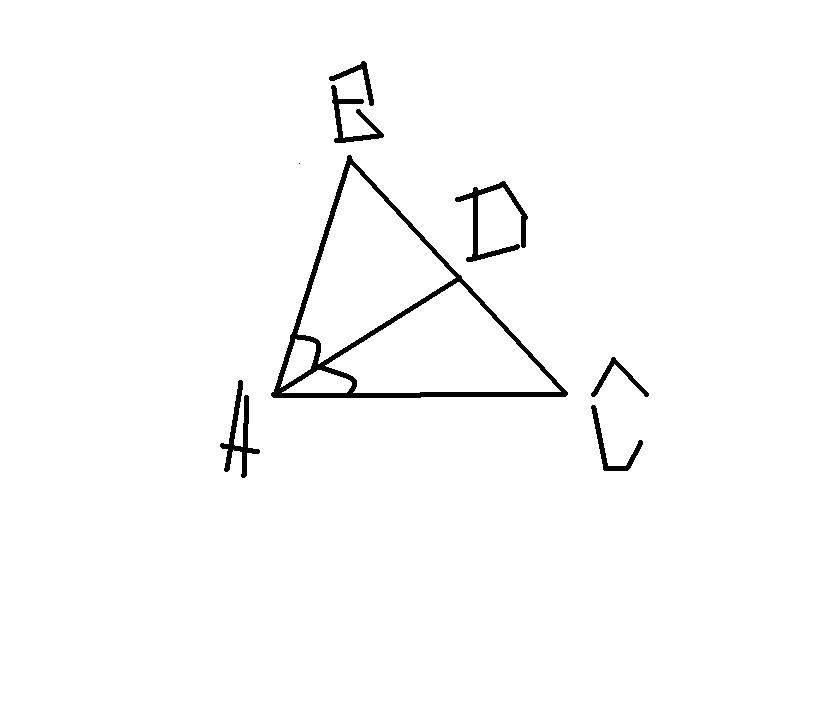
Похожие вопросы

Русский язык

2 года назад

Упр. 159. Выписать 3 причастия и сделать с этими причастиями морфологический разбор.

Другие предметы

2 года назад

1)средства труда-всё то...а)на что1)средства труда-всё то... а)на что направлен труд человека б)что является результатом труда в)при помощи чего человек трудится 2)производительность труда чем

Математика

7 лет назад

2м * 300см 8 дм* 100 мм 3000мм*2 м 50см 7000 м* 6км900м 4 км*5000м 20м *2000 см

Музыка

7 лет назад

Какая тональность в миноре параллельна тональности соль мажор

Математика

10 лет назад

скока будет 57,12 * 765 + (57869 *2) = ?

Математика

10 лет назад

Том купил с крючков ,а Гек х таких же крючков.Джо Гарпер записал такие выражения :с+х;с-х;с:х. Что хотел узнать Джо?

Математика

10 лет назад

Привет всем ! Помогите , пожалуйста .решить задачу ! Купили 8 коробок конфет,большие по 800 гр и маленькие по 400 гр ,всего 4 кг.Сколько коробок конфет каждого вида ?

Физика

10 лет назад

1)тепловая машина имеет максимальное кпд 50%.Определите температуру холодильника,если температура нагревателя 820 к