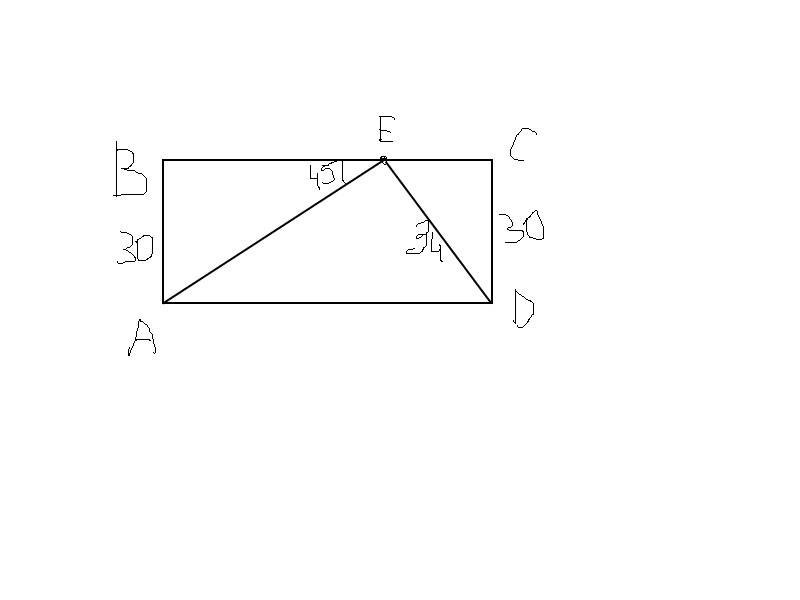
На стороне BC прямоугольника ABCD у которого AB= 30, отмечена точка Е так, что DE =34 и угол BEA =45 градусов. Найдите AD.

т.к. угол BEA=45, а угол EBA=90 (по условию - прямоугольник) , то угол BAE в треугольнике ABE равен тоже 45 (180-90-45). Это значит, что треугольник АВЕ равнобедренный (АВ=ВЕ=30). Треугольник ЕСD прямоугольный (угол ECD=90 градусов). Следовательно по теореме Пифагора (квадрат гипотенузы равен сумме квадратов его катетов) находим  отсюда EC==16.  BC=AD=BE+EC=30+16=46

очень пояснительный и хороший ответ спасибо