помогите пожалуйста,
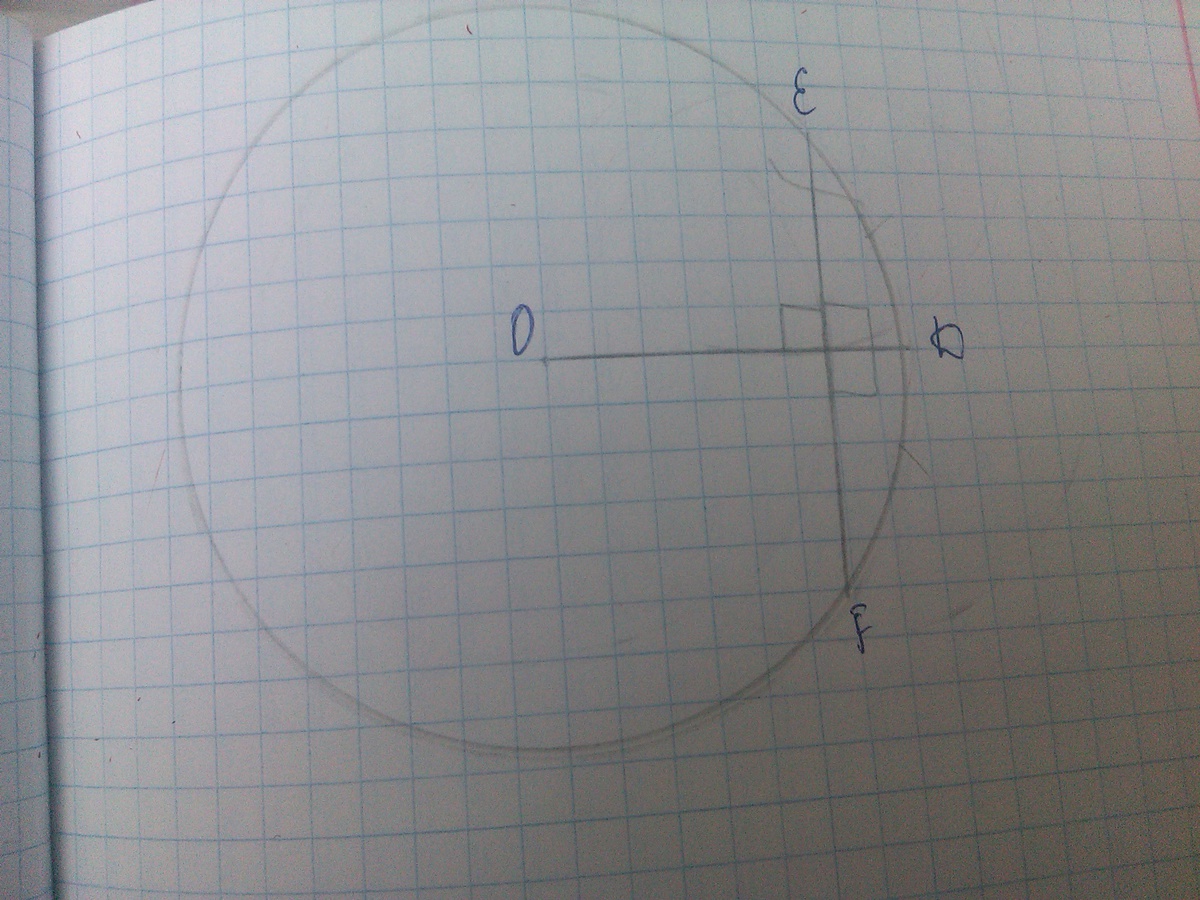
задана окружность с центром О и хордой EF, радиус ОД проведен перпендикулярно хорде EF. Докажите что хорда EF и DE равны.
Приложения:
Ответы
Ответ дал:
0
Данных в условии мало для доказательства равенства хорды и радиуса.
Теоретически хорда могла быть проведена на каком угодно расстоянии от центра при перпендикулярности к радиусу.
Теоретически хорда могла быть проведена на каком угодно расстоянии от центра при перпендикулярности к радиусу.
Ответ дал:
0
вот такое задание на контрольной у нас!
Ответ дал:
0
Треугольник LOM равнобедренный, т.к. ОL = OM = радиусу. Углы LOK и MOK равны , углы с пересечением с хордой прямые, значит треугольнички LOВ и МOD равны. Хорды LD = MD/ Значит и треугольнички LDK и MDK равны.Хорды LK и MK равны.
Ответ дал:
0
В - точка пересечения радиуса и хорды
Ответ дал:
0
Опечаточка. Пардон. Читать: "треугольнички LOD и МOD равны"
Ответ дал:
0
Читать : точка D перечечение с хордой
Похожие вопросы
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад