найдите угол между биссектрисой и медианой прямоугольного треугольника, которые проведены из вершины прямого угла.Если один из острых углов равен 20 градусам.
Ответы
Ответ дал:
0
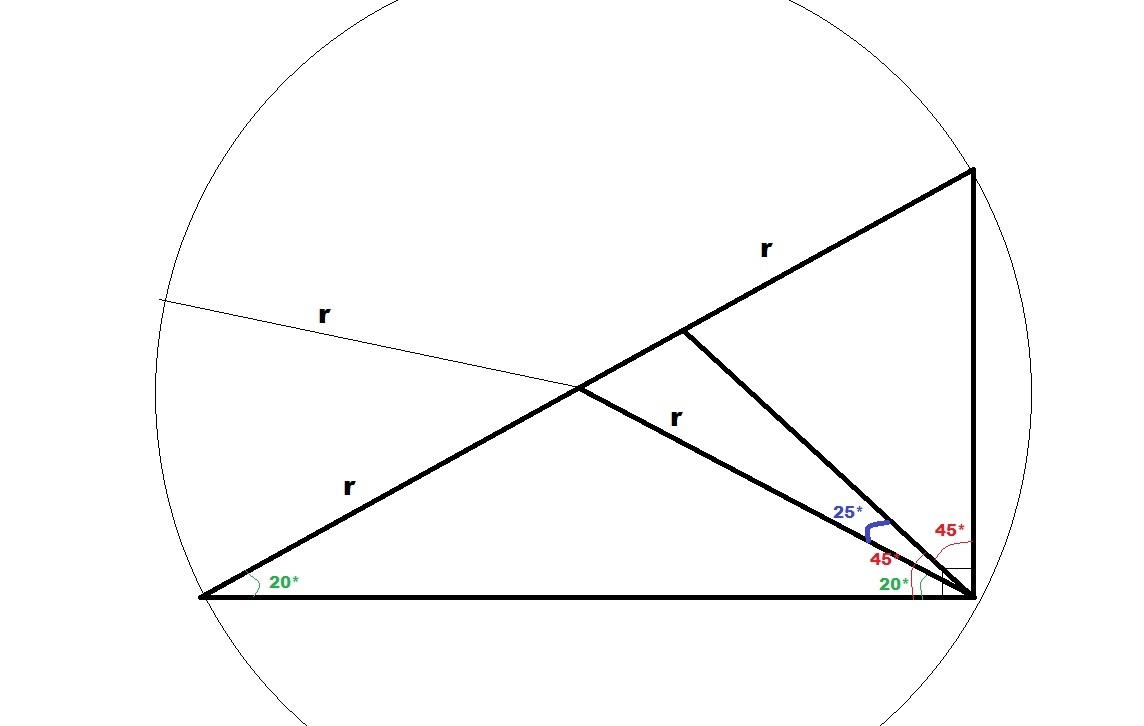
1) АВС- прямоугольный, угС=90* угА=20*, значит угАВС =70* ,СМ -медиана, СД биссектриса
рассмотрим треугольник АМС - равнобедренный, т к центр описаной окружности лежит на середине гипотенузы , т.е. АМ=АС=МВ . Следовательно уг МСА=20*
2) рассмотрим треугольник ДВС, угДСВ=45* по усл,
3) рассмотрим угАСВ=угАСМ+угМСД+угДСВ = 90* угАСВ= 20*+х+45*=90* х=25* угМСД=25*
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад