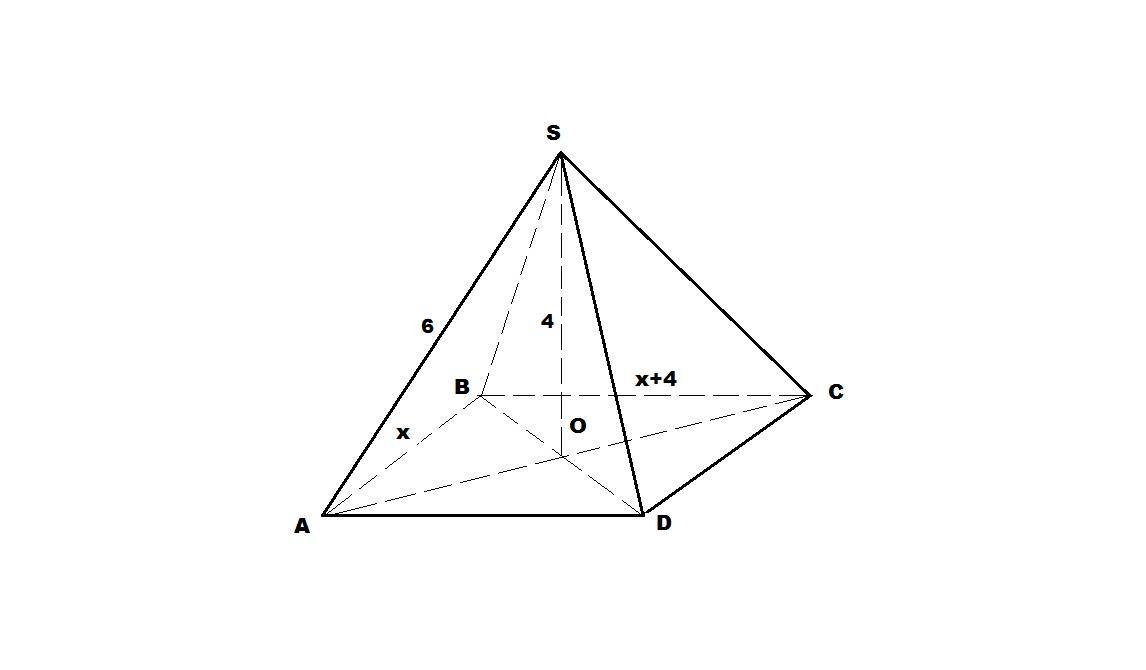
Точка S знаходиться на відстані 6см від кожної з вершин прямокутника ABCD і віддалена від його площини на 4 см. Знайти сторони прямокутника,якщо одна з них на 4см більша за другу.
Ответы
АВСД - прямоугольник, АС пересекается с ВД в точке О , О -проекция S на плоскость АВС ОS_|_ABC , ОА, ОВ,ОС,ОД - проекции соответственно SA, SB, SC, CD . OS=4cm , SA=SB=SC=SD=6cm
1) рассмотрим SOA -прямоугольный угО=90*, SO=4cm, SC=6cm
по тПифагора ОС= sqrt SC^2-SO^2 OC=2sqrt5 AC = 4sqrt5
2) рассмотрим треугольникАСД- прямоугольный угАДС=90* АС=4sqrt5 ,
пусть СД=х см АД=х+4 см
по тПифагора АС^2=x^2+(x=4)^2
2x^2+8x+16-(4sqrt5)^2 =0
x^2+4x-32=0
x1=4
x2=-8(не задовольняє)
ДС=4см
АД=4+4=8см
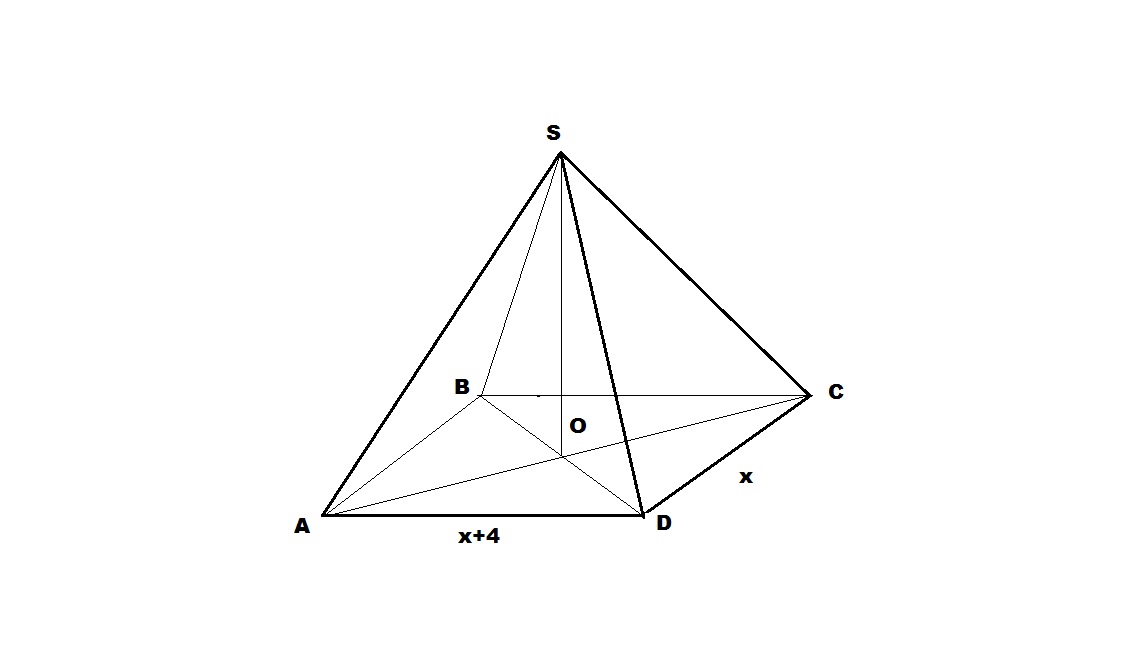
Ответ: 4см, 8 см.
Объяснение:
Пусть SO - перпендикуляр к плоскости прямоугольника.
SA = SB = SC = SD по условию.
Равные наклонные, проведенные из одной точки, имеют равные проекции, значит
ОА = ОВ = ОС = OD.
Тогда точка О - центр окружности, описанной около прямоугольника ABCD, т.е. точка пересечения его диагоналей.
SO = 4 см, SA = 6 см.
Из прямоугольного треугольника SOA по теореме Пифагора:
ОА = √(SA² - SO²) = √(36 - 16) = √20 = 2√5 cм
АС = 2ОА = 4√5 см
Пусть АВ = х, тогда ВС = х + 4.
Из прямоугольного треугольника АВС по теореме Пифагора составим уравнение:
АВ² + ВС² = АС²
x² + (x + 4)² = (4√5)²
x² + x² + 8x + 16 = 80
2x² + 8x - 64 = 0
x² + 4x - 32 = 0
По теореме, обратной теореме Виета:
х₁ = - 8 - не подходит по смыслу задачи,
х₂ = 4
АВ = 4 см
ВС = 4 + 4 = 8 см