Решить задачу
доказать, что ас перпендик. (АМВ)

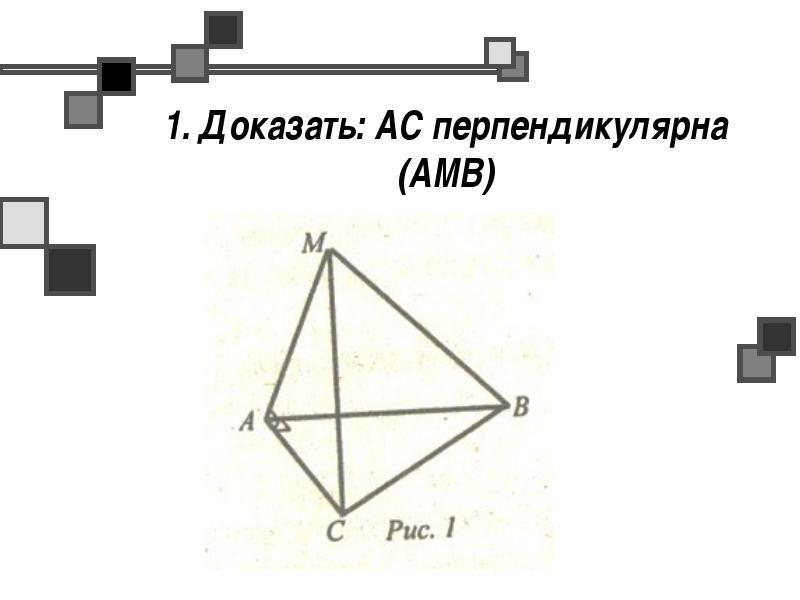
По рисунку очевидно, что АС ⊥ АМ и АС⊥АВ. Но АМ и АВ - пересекающиеся прямые, принадлежащие плоскости АМВ, значит по признаку перпендикулярности прямой и плоскости ("если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости") имеем что АС⊥(АМВ).
Что и требовалось доказать.