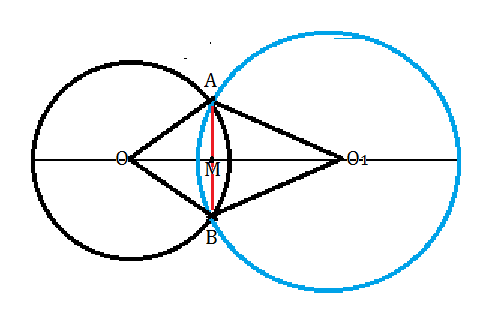
Окружности с центрами О и О1 пересекаются в точках А и В. Докажите что:Треугольник ОАО1=треугольнику ОВО1 ;2)треугольник ОАВ и треугольник О1АВ-равнобедренные.С рисунком нужно .

2) Треугольники АОВ и АО₁В - равнобедренные, так как в каждом две стороны равны как радиусы одной и той же окружности. 
1) Если провести к АВ высоту ОМ из О, то ОМ будет для  равнобедренного треугольника АОВ и медианой и биссектрисой.. 
Высота из О₁ в равнобедренном треугольнике АО₁В, проведенная к тому же отрезку АВ, тоже - медиана и биссектриса.  Так как М - середина одного и того же отрезка и углы при ней прямые, то М лежит на ОО₁  
Отсюда 
Угол АОМ=углу ВОМ, 
угол АО₁М=углу ВО₁М. 
ОО₁- общая сторона этих треугольников. 
По второму признаку равенства треугольников  треугольники равны, если у них равны два угла и сторона между ними. ⇒  Δ АО₁В=Δ АОВ ч.т.д.