Угол между биссектрисой и высотой,проведёнными из вершины наибольшего угла прямоугольного треугольника равен 14 градуса .Найдите углы треугольника

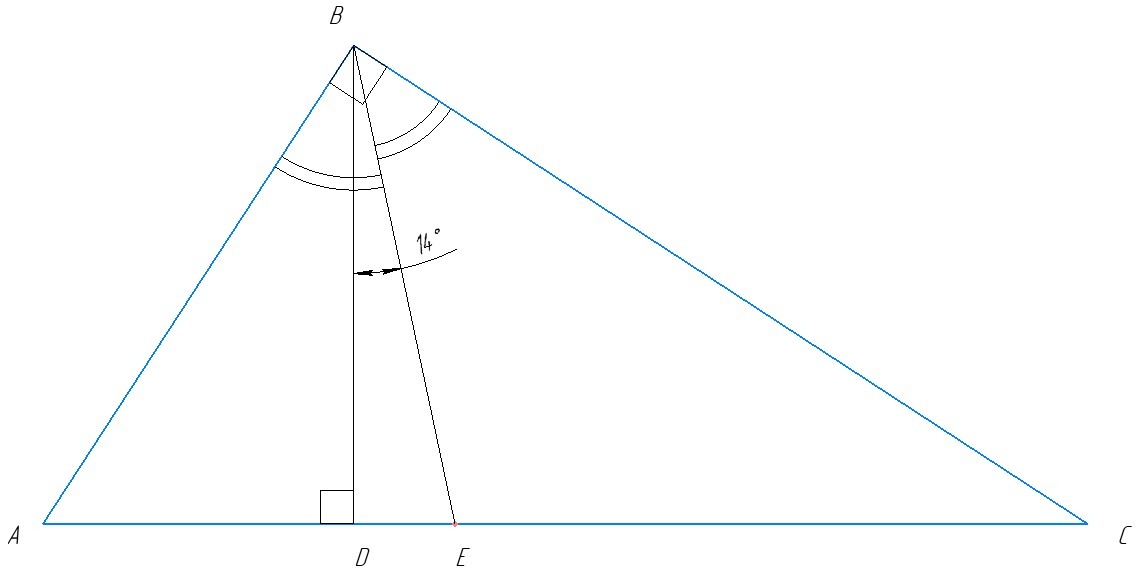
Для решения задачи сделаем рисунок (см. ниже)
ВЕ - биссектриса, BD  - высота, ∠ DBE = 14° по условию 
Так как ∠В = 90°, то
∠ABE = ∠EBC = 90° / 2 = 45°
С другой стороны ∠ABE = ∠ABD + ∠DBE
отсюда
∠ABD = ∠ABE - ∠ DBE = 45° - 14° = 31°

Из прямоугольного треугольника ΔABD найдем
∠А = 90° - ∠ABD = 90° - 31° = 59°

Из  ΔABC
∠C = 90° - ∠A = 90° - 59° =  31°

Ответ: ∠А = 59°
            ∠С = 31°
            ∠В = 90°